Реши задачу
На гранях тетраэдра
SABC провели медианы. Найди расстояние между
точками пересечения медиан граней ASB, BSC, если ребро тетраэдра равно 60.
Ответ???
Ответы
Ответ дал:
2
Ответ:
20
Объяснение:
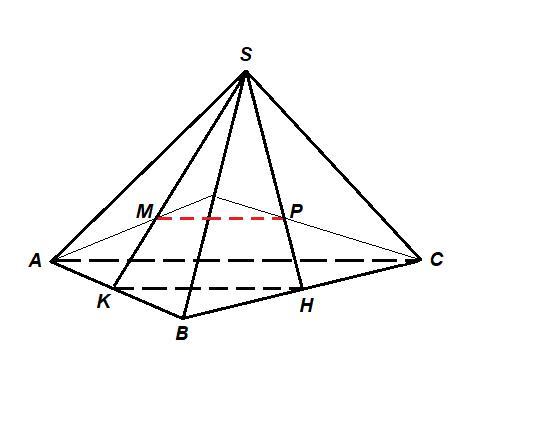
М - точка пересечения медиан грани ASB,
Р - точка пересечения медиан грани BSC.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины:
⇒
Тогда ΔMSP ~ ΔKSH по двум пропорциональным сторонам и углу (∠MSP общий).
KH = 0,5 · AC = 0,5 · 60 = 30 как средняя линия треугольника АВС.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад