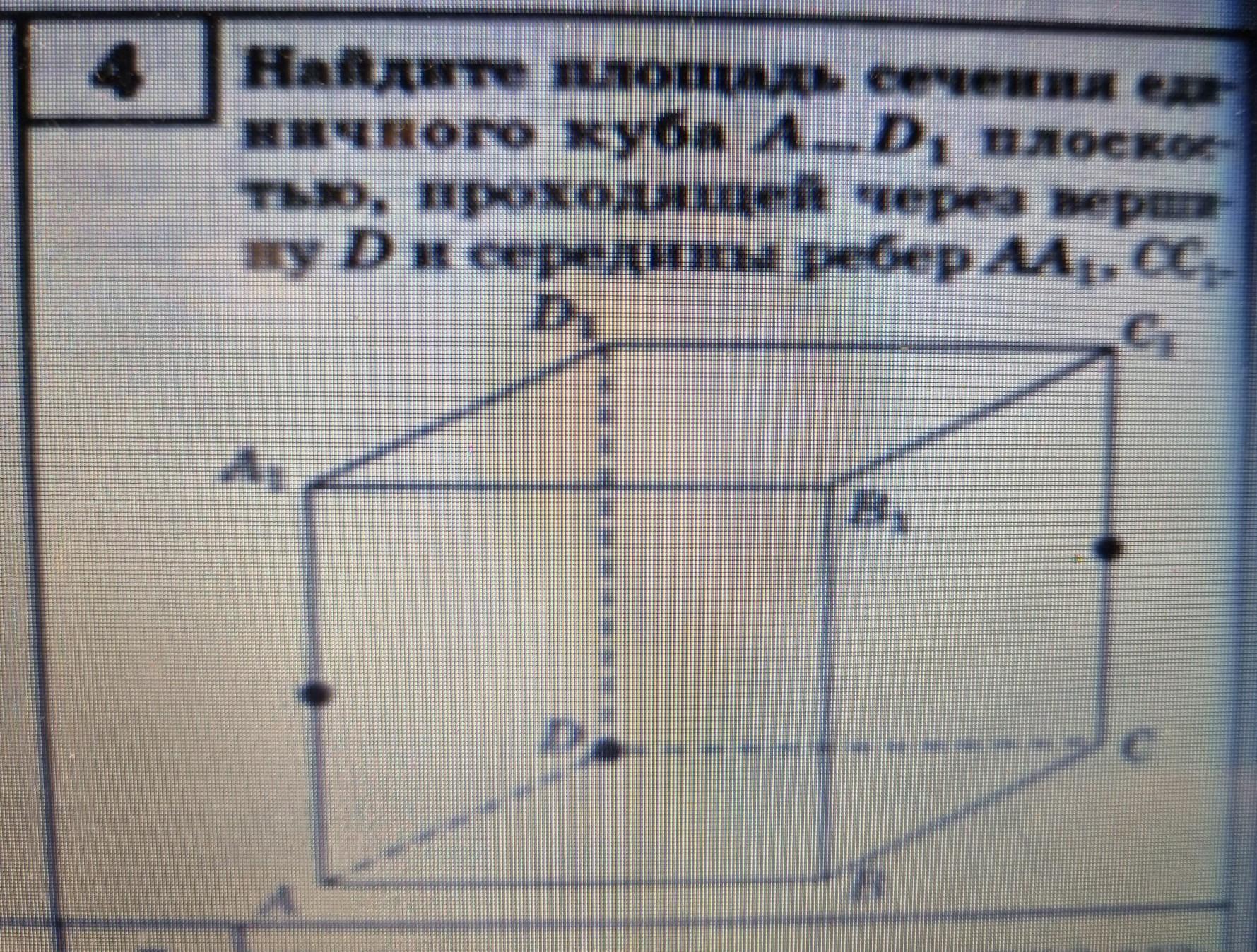
Срооочно Найдите площадь сечения единичного куба A...D1 плоскомтью,проходящей через точку D и середины AA1, CC1
Приложения:
Ответы
Ответ дал:
1
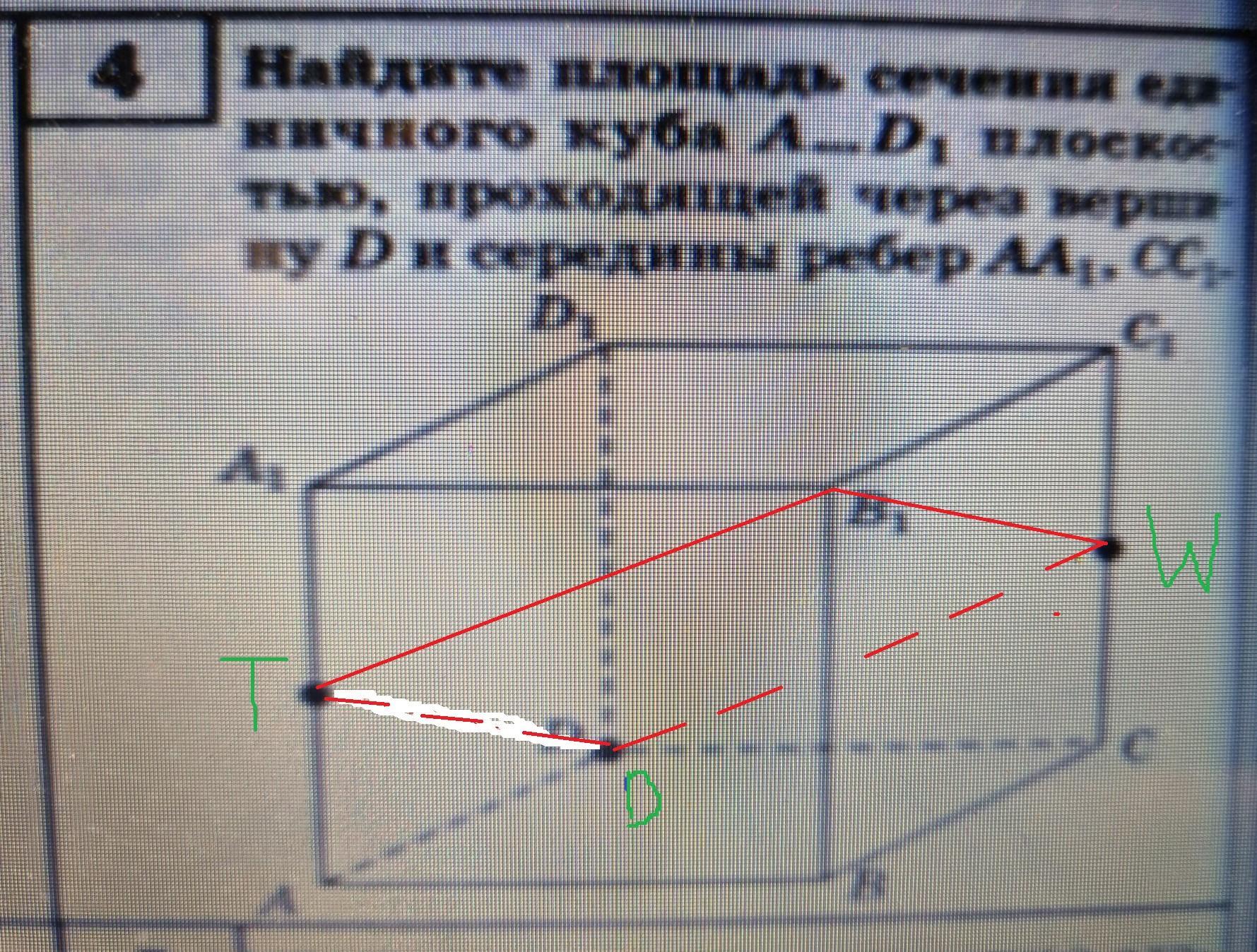
Так как TD║B₁W, то для построения сечения (см. рисунок) достаточно соединить четыре точки: T, D, B₁, W. Площадь данного прямоугольника равна: S₀ = TD * DW. В ΔTAD по теореме Пифагора: TD² = ТА² + АD² ⇒
TD² = 1² + =
⇒ TD = 0,5 * √5. Аналогично в ΔDWC: DW² = DС² + СW²
⇒ DW² = 1² + ⇒ DW = 0,5 * √5 ⇒ S₀ = 0,5 * √5 * 0,5 * √5 =
Ответ: площадь сечения равна 1,25 квадратных единиц
Приложения:
Petrograf:
есть ещё 1 задача, сможешь решить?
Найдите площадь сечения единичного куба A...D1 плоскомтью,проходящей через точку B и середины A1D1, D1C1
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад