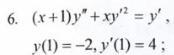Ответы
Ответ дал:
1
Обозначим .
Сразу найдем константу . По условию
.
Возвращаемся к .
Итого,
.
Теперь стоит вспомнить, что в самом начале решения мы делили на . Убедимся, что
не является решением данной задачи.
Действительно,
Однако
Ответ.
Вас заинтересует
11 месяцев назад
11 месяцев назад
1 год назад
1 год назад
7 лет назад
8 лет назад