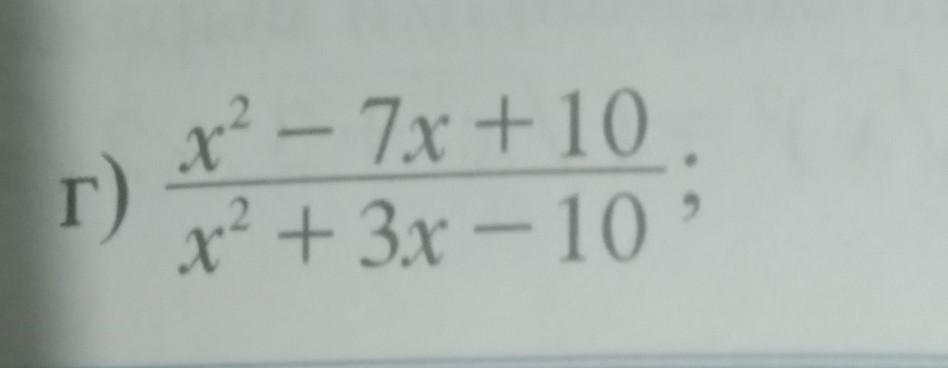Ответы
Ответ:
Объяснение:
Ответ:
Объяснение:
Мне если честно теорема Виета не сильно нравится, я обычно пользуюсь такой формулой
x1+x2 = b
x1 * х2 = с
так найдя х1 и х2 можно сразу разложить уравнение на множители и если надо, исходя из этого искать корни.
---------------------------------------------------
Можно использовать теорему Виета где
x1+x2 = -b (в данном случае это -7, и 3 и т.к - на - дает плюс, ищем +7 и -3)
x1 * х2 = с (в данном случае это 10 и -10)
5 + 2 в сумме дают 7, и при умножении 10, поэтому они являются корнями первого квадратного уравнения
-5 и 2 в сумме дают -3 и при умножении -10 поэтому они являются корнями второго квадратного уравнения
далее квадратное уравнение можно разложить на множители в таком виде
(х-х1)(х-х2)
то есть в числителе у нас будет (х-5)(х-2)
а в знаменателе (х+5)(х-2)
после чего (х-2) можно сократить.