Question

К окружности проведена касательная так, что один из концов диаметра удалён от нее на 16 см . Найдите расстояние до другого конца диаметра , если радиус окружности равен 23 см

Answer 1

Ответ:

30 см

Пошаговое объяснение:

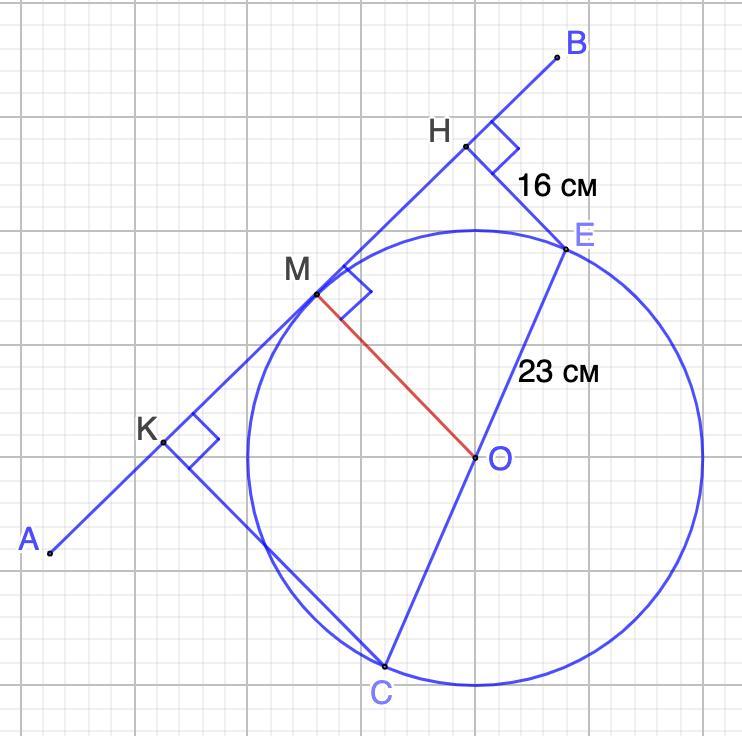
Дано: Окр. О, ОЕ;

АВ - касательная;

ЕН = 16 см; ОЕ = 23 см.

Найти: СК

Решение:

Проведем АМ - радиус в точку касания.

1. Рассмотрим СКНЕ

• Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.

⇒ ЕН ⊥ АВ, СК ⊥ АВ.

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ НЕ || СК

• Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

⇒ СКНЕ - прямоугольная трапеция.

2. ОЕ = ОС = R;

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОМ ⊥ АВ

⇒ АВ || НЕ || СК

• Если отрезок в трапеции проходит через середину одной из его боковых сторон, пересекает вторую и параллелен основаниям — этот отрезок можно назвать средней линией этого трапеции.

⇒ ОМ - средняя линия трапеции СКНЕ.

ОМ = ОЕ = ОС = 23 см (радиусы)

• Средняя линия трапеции равна полусумме оснований.

$\displaystyle OM=\frac{HE+CK}{2}\\\\23 = \frac{16+CK}{2}\\\\16+CK = 46\\\\CK= 30$

CK = 30 см