Question

Найти площадь фигуры, ограниченной линиями: y=(x+1)^2, y^2=x+1
Нужно с пояснением, пошагово.

Answer 1

Ответ:

$\displaystyle S=\frac{1}{3}$  ед².

Пошаговое объяснение:

$\displaystyle y_1= (x+1)^2\;\;\;u \;\;\;y_2^2=x+1 \;\;\;$

Преобразуем второй график:

$\displaystyle y_2=^+_-\sqrt{x+1}$

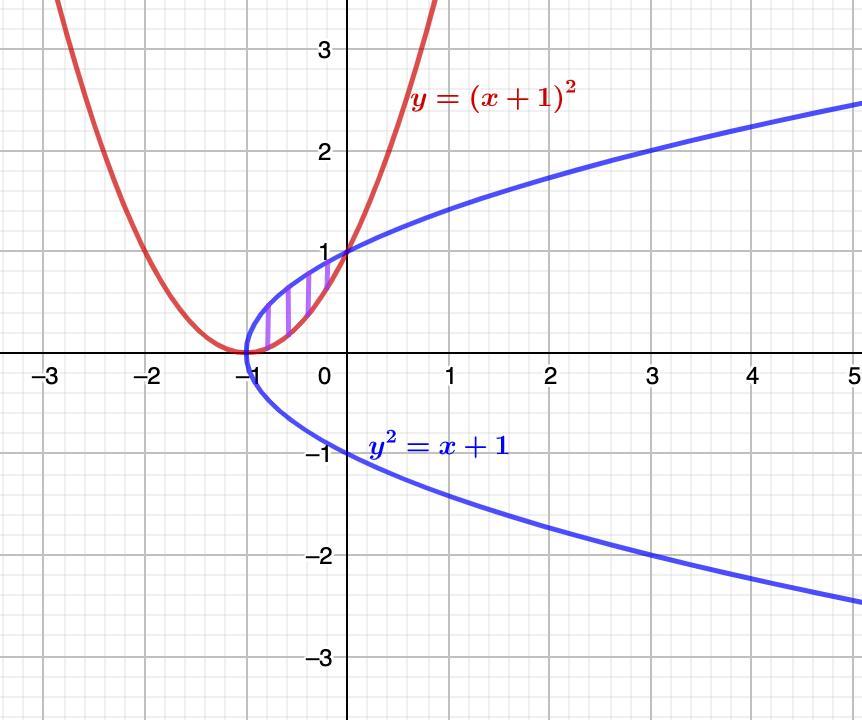
Так как первый график - парабола, у которой ветви направлены вверх и вершина имеет координаты (-1; 0), то данный график расположен выше оси 0х, то есть y≥0, то у второго графика будем рассматривать только ветвь параболы

$y=\sqrt{x+1}$

Найдем точки пересечения.

$\displaystyle \left \{ {{y=(x+1)^2} \atop {y=\sqrt{x+1} }} \right. \\\\ODZ:x\geq -1\\\\(x+1)^2=\sqrt{x+1}\;\;\;\;\;\\(x+1)^4=x+1 \\(x+1)((x+1)^3-1)=0\\(x+1)(x+1-1)((x+1)^2+(x+1)+1)=0\\\\(x+1)*x*(x^2+3x+3)=0\\x_1=-1;\;\;\;x_2=0$

Площадь фигуры, ограниченной линиями:

$\displaystyle S=\int\limits^{x_2}_{x_1} {(f_2(x)-f_1(x))} \, dx$

Имеем:

$\displaystyle f_2(x)=\sqrt{1+x} ;\;\;\;f_1(x)=(x+1)^2;\;\;\;x_2=0;\;\;\;x_1=-1$

$\displaystyle S=\int\limits^0_{-1} {(\sqrt{x+1}- (x+1)^2) } \, dx$

Замена переменной:

х+1 = t

dx=dt

Меняем пределы интегрирования

x=-1; t=0

x=0; t=1

Получим:

$\displaystyle S= \int\limits^1_0 {(t^{\frac{1}{2} }-t^2)} \, dt=( \frac{2t^{\frac{3}{2} }}{3} -\frac{t^3}{3})\left|^1_0=\frac{2}{3}-\frac{1}{3}=\frac{1}{3}$   (ед²)