Question

помогите пожалуйста. Дам 25 балов

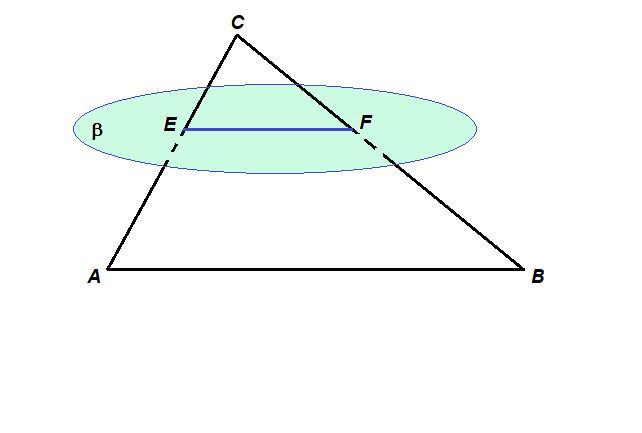
плоскость бета пересекает стороны AC и BC треугольника ABC в точках E и F соответственно и параллельна стороне, AB, AE : CE = 5 : 2, AB = 21 см. Найдите отрезок EF. ​

Answer 1

Ответ:

EF = 6 см

Объяснение:

АВ║β, плоскость треугольника пересекает плоскость β по прямой EF, значит линия пересечения параллельна АВ,

EF║AB.

∠CEF = ∠CAB как соответственные при пересечении EF║AB секущей АС, ∠С - общий для ΔECF и ΔАСВ, значит

ΔECF ~ ΔАСВ по двум углам.

$\dfrac{EF}{AB}=\dfrac{EC}{AC}$

AE : EC = 5 : 2, значит ЕС состоит из двух равных частей, а АЕ - из пяти, тогда

$\dfrac{EC}{AC}=\dfrac{2}{7}$

$\dfrac{EF}{21}=\dfrac{2}{7}$

$EF=\dfrac{21\cdot 2}{7}=3\cdot 2=6$ см