Ответы
Ответ дал:
1
Ответ:
4√3 см
Объяснение:
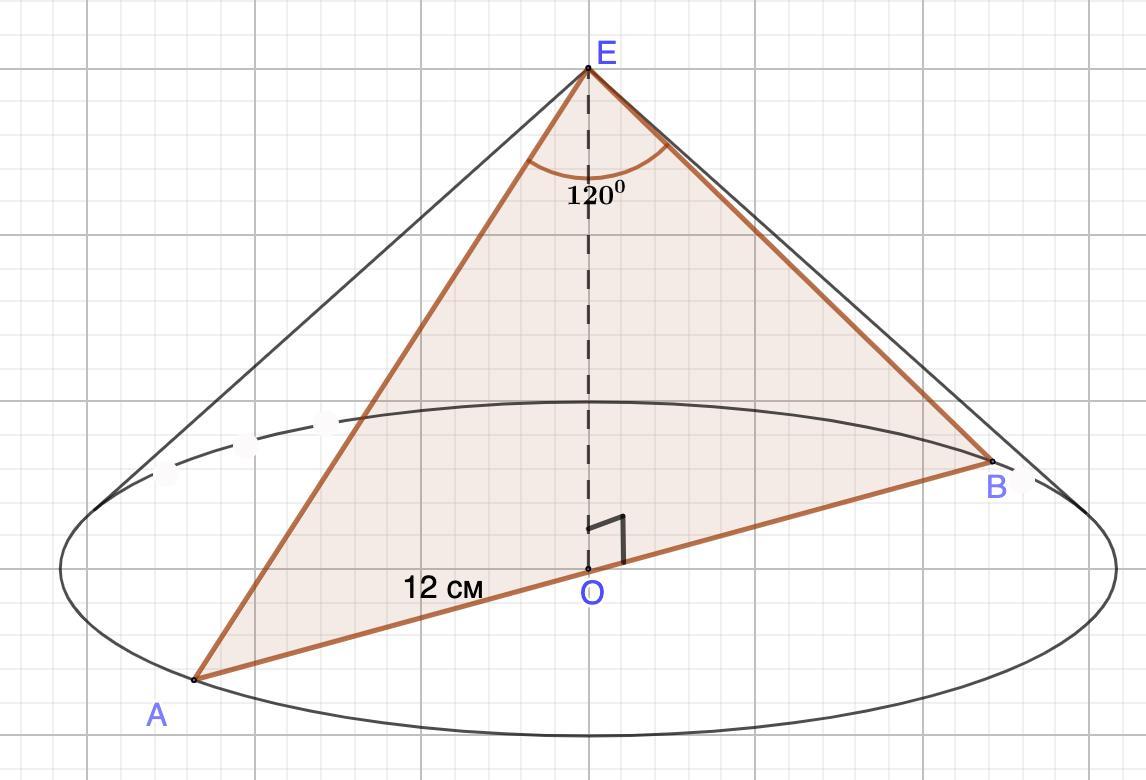
Дано: конус.
АЕВ - осевое сечение.
∠АЕВ = 120°
АО = 12 см - радиус основания.
Найти: ЕО
Решение:
- Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.
⇒ ΔАЕВ - равнобедренный.
- В равнобедренном треугольнике высота , проведенная к основанию,
- является биссектрисой.
⇒ ∠АЕО = ∠ОЕВ = 120°:2 = 60°
Рассмотрим ΔАЕО - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ЕАО = 90° - °АЕО = 90° - 60° = 30°
Пусть ОЕ = х см
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ АЕ = 2х см
По теореме Пифагора:
⇒ ЕО = 4√3 см
Приложения:
sofiya2704:
дякую!
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад
