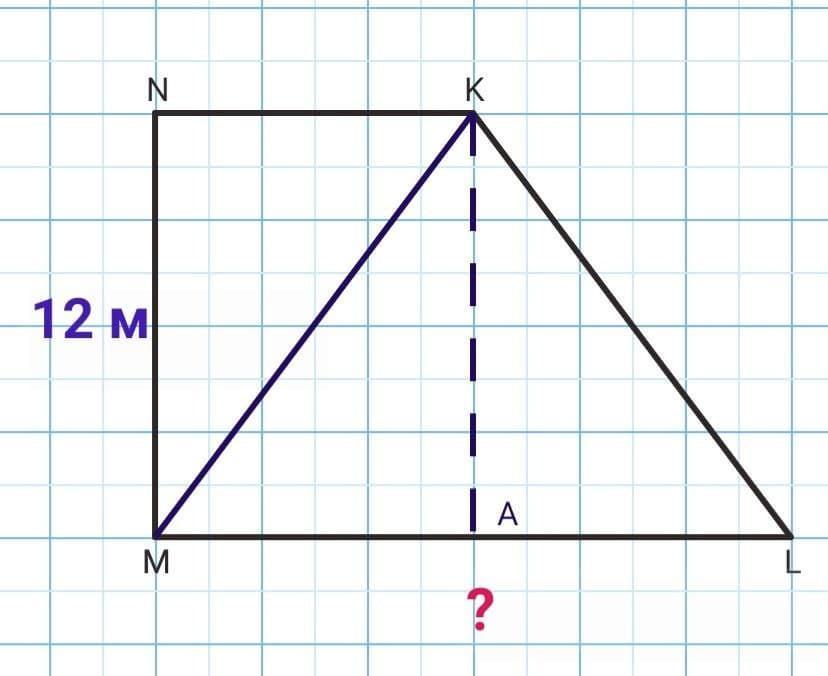
Найди длину большего основания ML прямоугольной трапеции MNKL, где уголM = 90°. Сторона MN = 12 м, диагональ MK = 13 м, S треугольника MKL = 120 м^2.
срочно
Ответы
Ответ дал:
0
Ответ:
20м
Объяснение:
- Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h):
AK - высота прямоугольной трапеции MNKL. AK = MN = 12 м (как стороны прямоугольника MNKА), ⇒
Приложения:
selniknik74:
неверно
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад