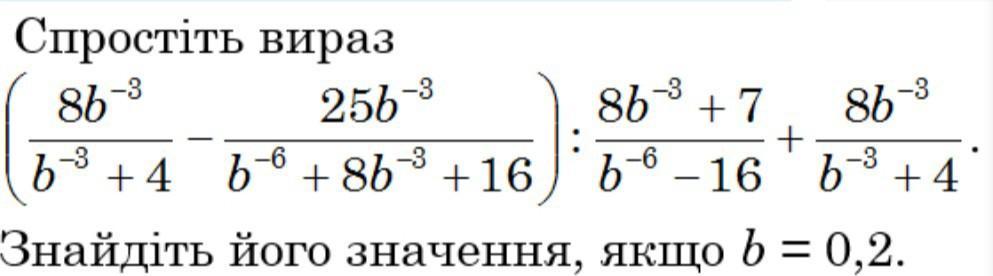Ответы
Ответ дал:
1
Ответ:
125
Объяснение:
Пусть . Тогда выражение примет следующий вид:
Возвращаясь к замене, получим
xenia2022:
Спасибо
Вас заинтересует
2 года назад
8 лет назад
9 лет назад