Question

ДАЮ МНОГО БАЛЛОВ!!!!!!!
Помогите пожалуйста!!!!
Задания на фото!!!!!

Answer 1

Ответ:

Объяснение

Почленно делим числитель на знаменатель.Чтобы разделить выражение в корне,возводим делитель в квадрат и делим подкоренное выражение на 4.

$x^{2} +22x-8=0\\x_{2} =\frac{-22-\sqrt{22^{2} -4*(-8)} }{2} \\x_{2} ={-11-\sqrt{(22^{2} +2):2^{2} } } \\x_{2} ={-11-\sqrt{(484+32):4 } } \\x_{2} ={-11-\sqrt{129 } } \\\\x_{1} =\frac{-22+\sqrt{22^{2} -4*(-8)} }{2} \\x_{1} ={-11+\sqrt{(22^{2} +2):2^{2} } } \\x_{1} ={-11+\sqrt{(484+32):4 } } \\x_{1} ={-11+\sqrt{129 } }$

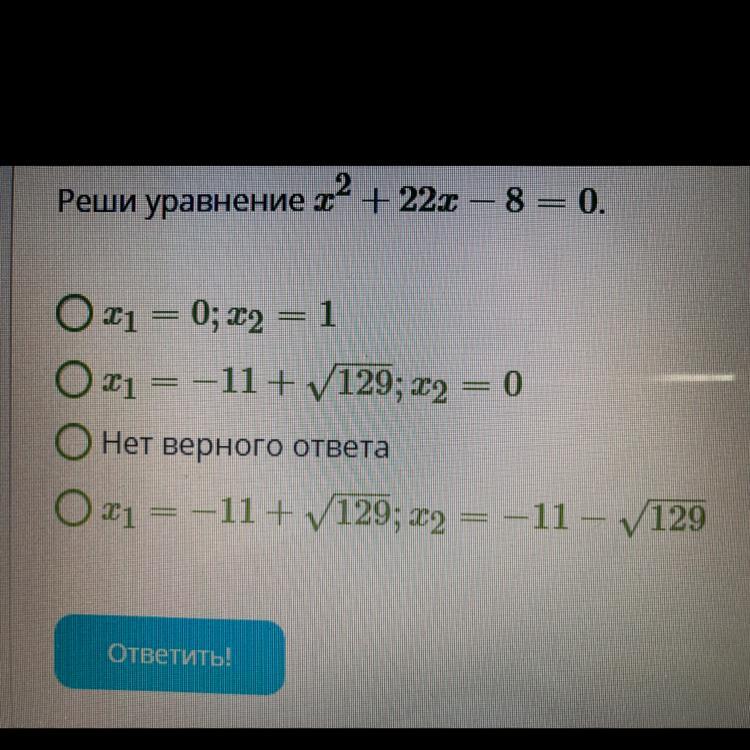
Верный вариант ответа последний

$\\x_{1} ={-11+\sqrt{129 } } \\\\ \\x_{2} ={-11-\sqrt{129 } }$

Answer 2

Ответ:

$x {}^{2} + 22x - 8 = 0 \\ a = 1~~~~~~~~~b = 22~~~~~~~~~c = - 8 \\ D=b {}^{2} - 4ac = 22 {}^{2} - 4 \times 1 \times ( - 8) = 484 + 32 = 516 \\ x1 = \frac{ - 22 + \sqrt{516} }{2 \times 1} = \frac{ - 22 + 2 \sqrt{129} }{2} = \frac{2(11 + \sqrt{129)} }{2} = - 11 + \sqrt{129} \\ x2 = \frac{ - 22 - \sqrt{516} }{2 \times 1} = \frac{ - 22 - 2 \sqrt{129} }{ 2 } = \frac{2( - 11 - \sqrt{129)} }{2} = - 11 - \sqrt{129}$

Ответ последний.