Срочно помогите!
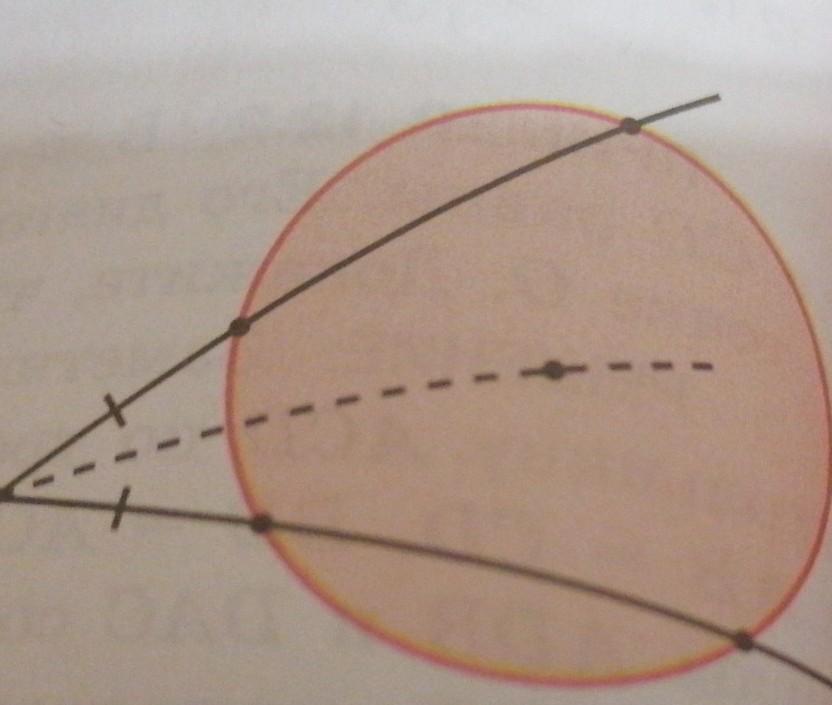
окружность пересекают стороны угла в четырех точках оказалось что две из них находятся на равном расстоянии от его вершины. Докажите что центр этой окружности лежит на биссектрисе данного угла

Приложения:

Ответы

Ответ дал: vikll

Ответ:

Объяснение:

окружность пересекают стороны угла в четырех точках оказалось что две из них находятся на равном

Приложения:

vikll: Можно и через равенство тр-ков АВО и АСО по 3-му признаку .Значит угол ВАО=САО, как соответственные углы равных тр-ков, т.е АО- биссектриса угла ВАО по определению.

Ответ дал: siestarjoki

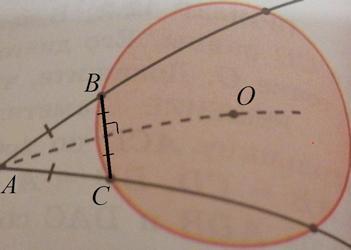
Проведем хорду BC.

Центр окружности O лежит на серединном перпендикуляре к хорде BC.

Вершина A равнобедренного △BAC лежит на серединном перпендикуляре к основанию BC.

То есть прямая AO является серединным перпендикуляром к BC.

В равнобедренном треугольнике серединный перпендикуляр к основанию является биссектрисой.

AO - биссектриса угла A.

Приложения: