Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Рассмотрим первое слагаемое.
Подкоренное выражение неотрицательно!
Рассмотрим второе слагаемое.
На 0 делить нельзя!
Объединим решения:
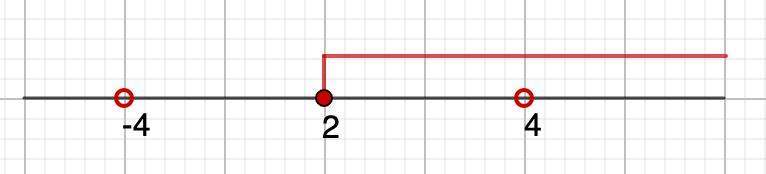
х ∈ [2; 4) ∪ (4; +∞)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад