Ответы
Ответ дал:
3
Ответ:
Объяснение:
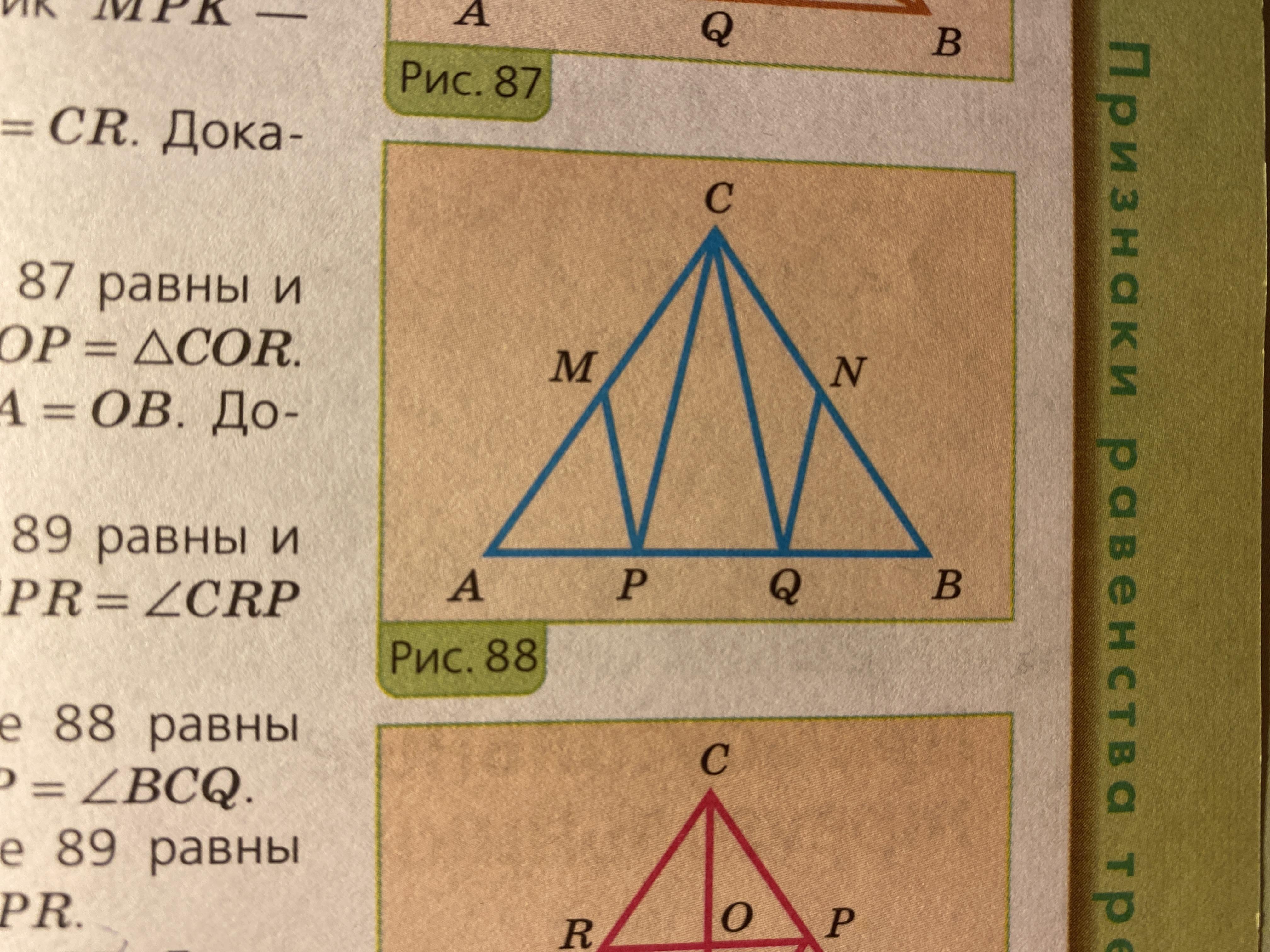
по условию AQ=PB, значит, AP=QB, тр-к CPQ -равнобедр-й, т.к. углы при основании равны, и значит, РС=CQ. < CPA = <CQB (как смежные равных углов AQC u BPC, ), значит, тр-к ACP= тр. BCQ пот 1-му признаку и следовательно < ACP = <BCQ
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад