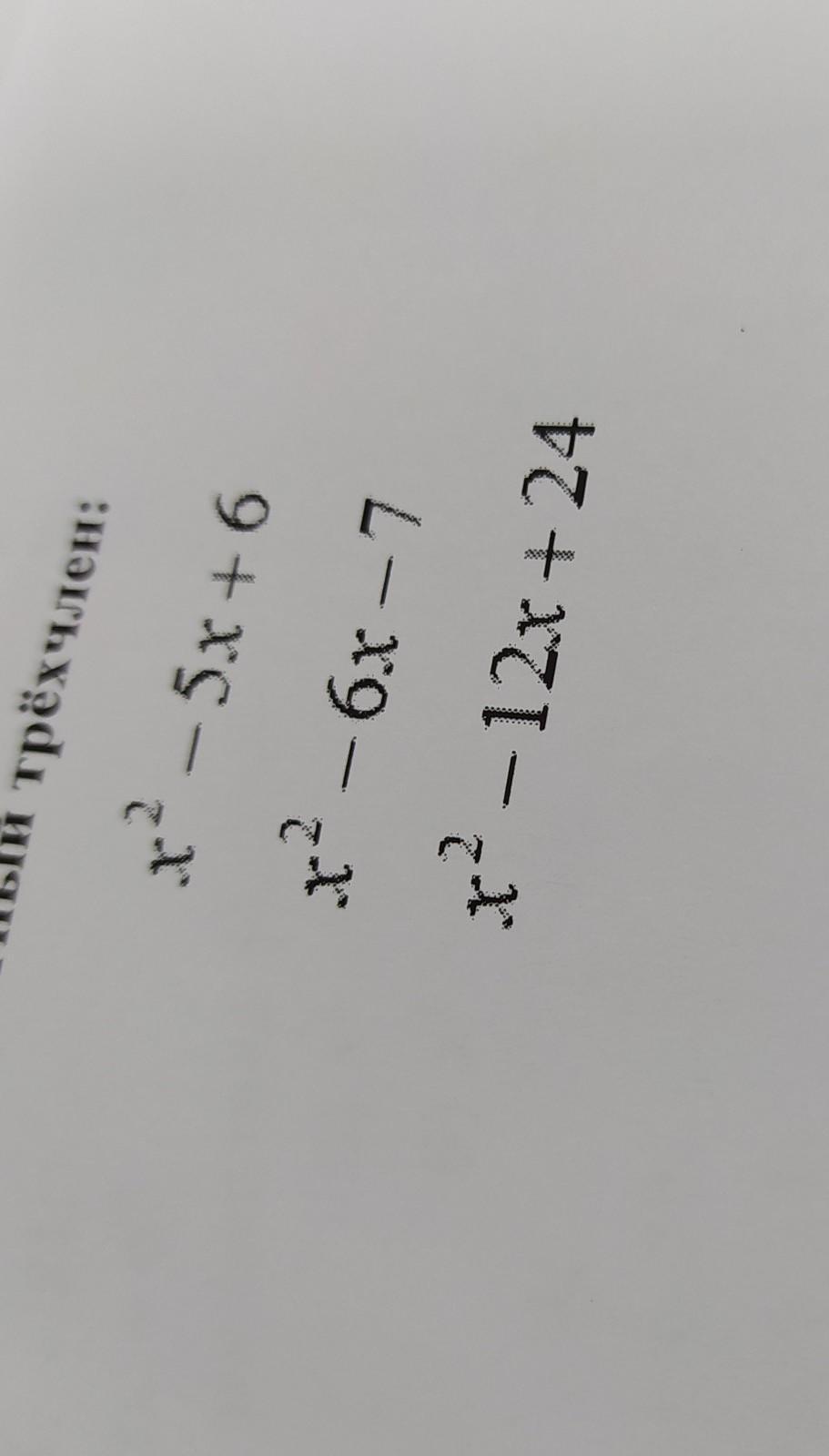Ответы
Ответ дал:
0
1) (х-2)(х-3)
2) (х-7)(х+1)
3) D = 144 - 96 = 48
получается вот так, но скорее всего там небольшая ошибка (в трехчлене, а не решении)
формула по которой я разложила первые трехчлены
формулы дискриминанта
и тогда трехчлен можно разложить на множители таким способом
birindzoglyalina:
Эх, могли бы раньше помочь :'(
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад