Решите пожалуйста по образцу!!!
Радиус окружности, вписанной в правильный многоугольник, равен
12 см, а сторона многоугольника — 8 3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника
Приложения:

Ответы
Ответ дал:
1
Центр вписанной в угол окружности лежит на биссектрисе. Окружности, вписанной в правильный многоугольник - в точке пересечения биссектрис его углов.
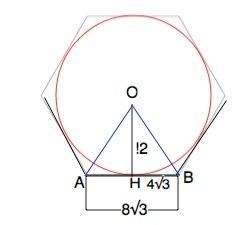
На рисунке приложения АВ - сторона, АО=ВО - биссектрисы углов правильного многоугольника. ОН - радиус вписанной окружности,
tg∠ОВН=ОН:ВН=√3. ⇒ Угол ОВН=60°, угол многоугольника 120°, смежный с ним внешний угол равен 60°.
Сумма внешних углов многоугольника 360°. Количество внешних углов, взятых по одному при вершинах, равно числу сторон многоугольника.
Число сторон 360°:60°=6.
Радиус описанной около правильного шестиугольника окружности равен его стороне.
R=8√3
C=2πR=16√3π
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад