100 БАЛЛОВ Напиши уравнение окружности, которая проходит через точку 7 на оси Ox и через точку 10 на оси Oy, если известно, что центр находится на оси Ox.
(Дроби максимально сократите. Если в ответе получилось целое число, то запишите его в виде дроби со знаменателем 1.)
Приложения:
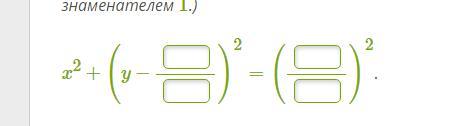
Ответы
Ответ дал:
0
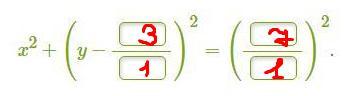
Думаю так - правильно
Приложения:
dimaplatonov1123:
Смотря на прошлые задания я усвоил что там не может быть 1 (
Нужно не смотреть на прошлые задания, а подставить в уравнение координаты данных точек.
И если при этом уравнение обратится в верное тождество, то значит, что уравнение найдено верно.
А в данном случае ни 7^2+(0-3)^2 не равно 7. Поэтому это уравнение - неверное.
Можешь так же с другой задачой такого же смысла помочь?)
Ответ дал:
1
Ответ: (x+51/14)²+y²=(149/14)²
Объяснение:
Запишем уравнение окружности в виде (x-a)²+(y-b)²=R², где a и b - координаты центра окружности, R - её радиус. Так как по условию центр окружности находится на оси ОХ, то b=0. Тогда уравнение окружности принимает вид: (x-a)²+y²=R². Подставляя в это уравнение координаты данных точек, получаем систему уравнений:
(7-a)²+0²=R²
(0-a)²+10²=R²,
или:
(7-a)²=R²
a²+100=R²
Решая её, находим a=-51/14 и R²=(149/14)². Поэтому искомое уравнение окружности таково: (x+51/14)²+y²=(149/14)²
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад