Условие задания.
Квадрат ABCD со стороной а = 7 расположен так, что координаты вершины А
равны (-2; 3). Вычисли координаты остальных вершин, если известно, что сторона
квадрата AB параллельна оси ординат и начало координат лежит внутри квадрата.
Ответ:
вершины квадрата: В
С(
1);
DO
Ответить!
Ответы
Ответ:
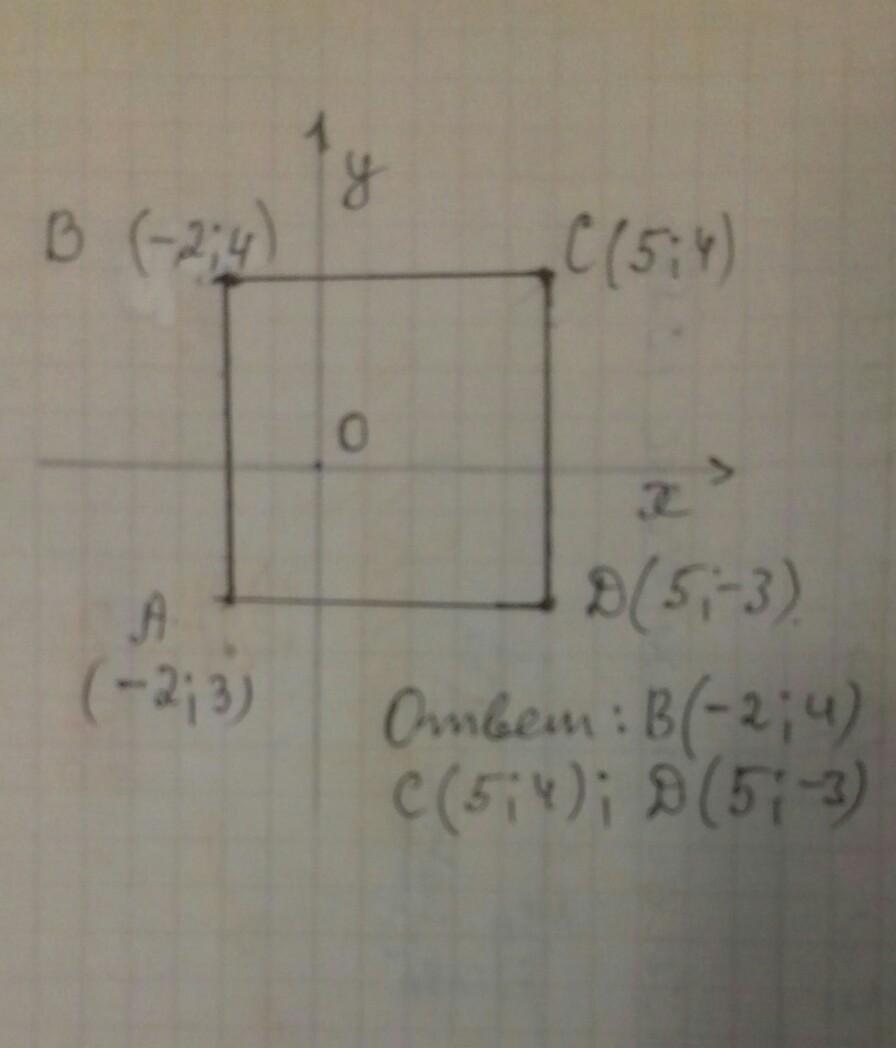
Вершины квадрата: В(-2;-4), С(5;-4), D(5;3)
Объяснение:
А(-2;3)
а=7
1) Известно, что сторона квадрата AB параллельна оси ординат, значит, абсцисса точки В равна -2.
2) Известно также, что начало координат лежит внутри квадрата, значит, точка В лежит ниже оси Ох на расстоянии равном 7-3=4. Следовательно, можно записать координаты точки В(-2;-4).
3) Находим координаты точки С. Её ордината совпадает с ординатой точки В и равна -4. Т.к. АВСД - квадрат, то точка С лежит на прямой, параллельной оси Ох, на расстоянии равном 7-2=5 от оси Оу. Следовательно, её координаты С(5;-4).
4) Осталось записать координаты точки D. Её абсцисса совпадает с абсциссой точки С, а ордината совпадает с ординатой точки А. Значит, D(5;3)
Ответ:
.......................................