Question

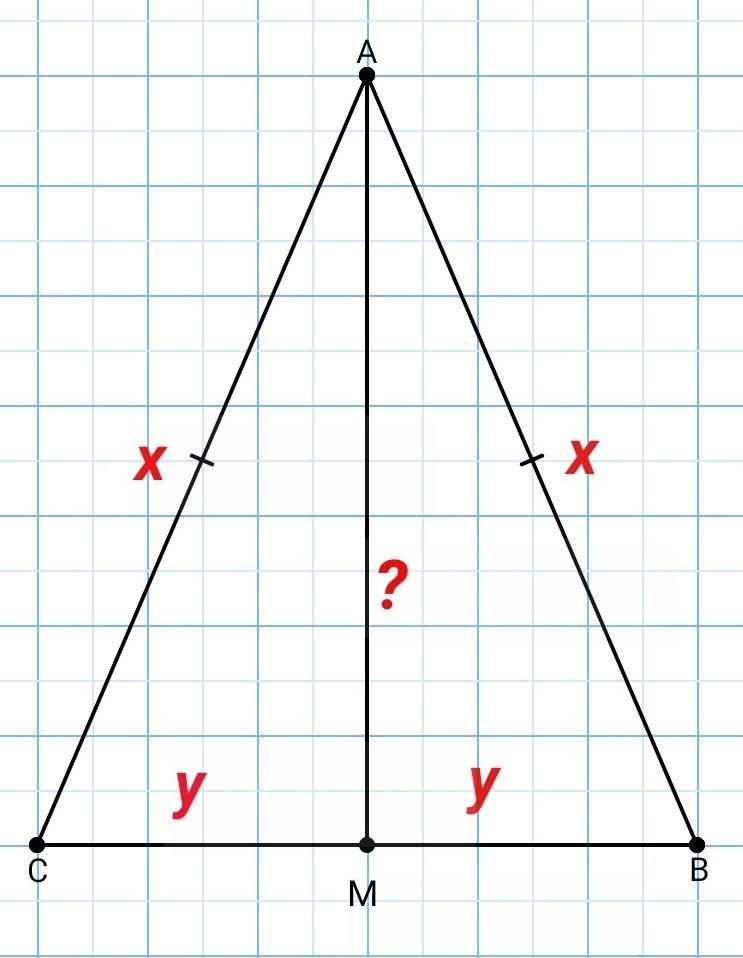
в равнобедренном треугольнике ABC с основанием BC проведена медиана AM. Найдите медиану AM,если периметр треугольника ABC равен 40см,а периметр треугольника ABM равен 32см.​

Answer 1

Ответ:

12см

Объяснение:

Треугольник АВС- равнобедренный. АВ=АС= х см

АМ - медиана. => СМ=МВ= у см

Р(АВС)=АВ+АС+ВС=2х+2у=40

=> х+у=20. у=20-х

Так как медиана в равнобедренном треугольнике является высотой, то треугольник АВМ - прямоугольный, угол М=90°.

По т.Пифагора АМ=

$\sqrt{ {x}^{2} - {y }^{2} } = \sqrt{ {x}^{2} - {(20 - x)}^{2} } = \sqrt{ {x}^{2} - 400 + 40x - {x}^{2} } = \sqrt{40x - 400}$

Р(АМВ)= АМ+АВ+МВ = 32

$\sqrt{40x - 400} + x + (20 - x) = 32 \\ \sqrt{40x - 400} = 12 \\ 40x - 400 = 144 \\ 40x = 544 \\ x = 13.6$

АВ=АС=13,6 см

МВ=у=20-13,6=6,4 см

АМ=

$\sqrt{ {x}^{2} - {y}^{2} } = \sqrt{ {13.6}^{2} - {6.4}^{2} } = \sqrt{184 - 40.96} = \sqrt{144} = 12$

АМ=12см