За формулою Ньютона-Лейбніца, обчислини інтеграл. Детально розписати
Приложения:
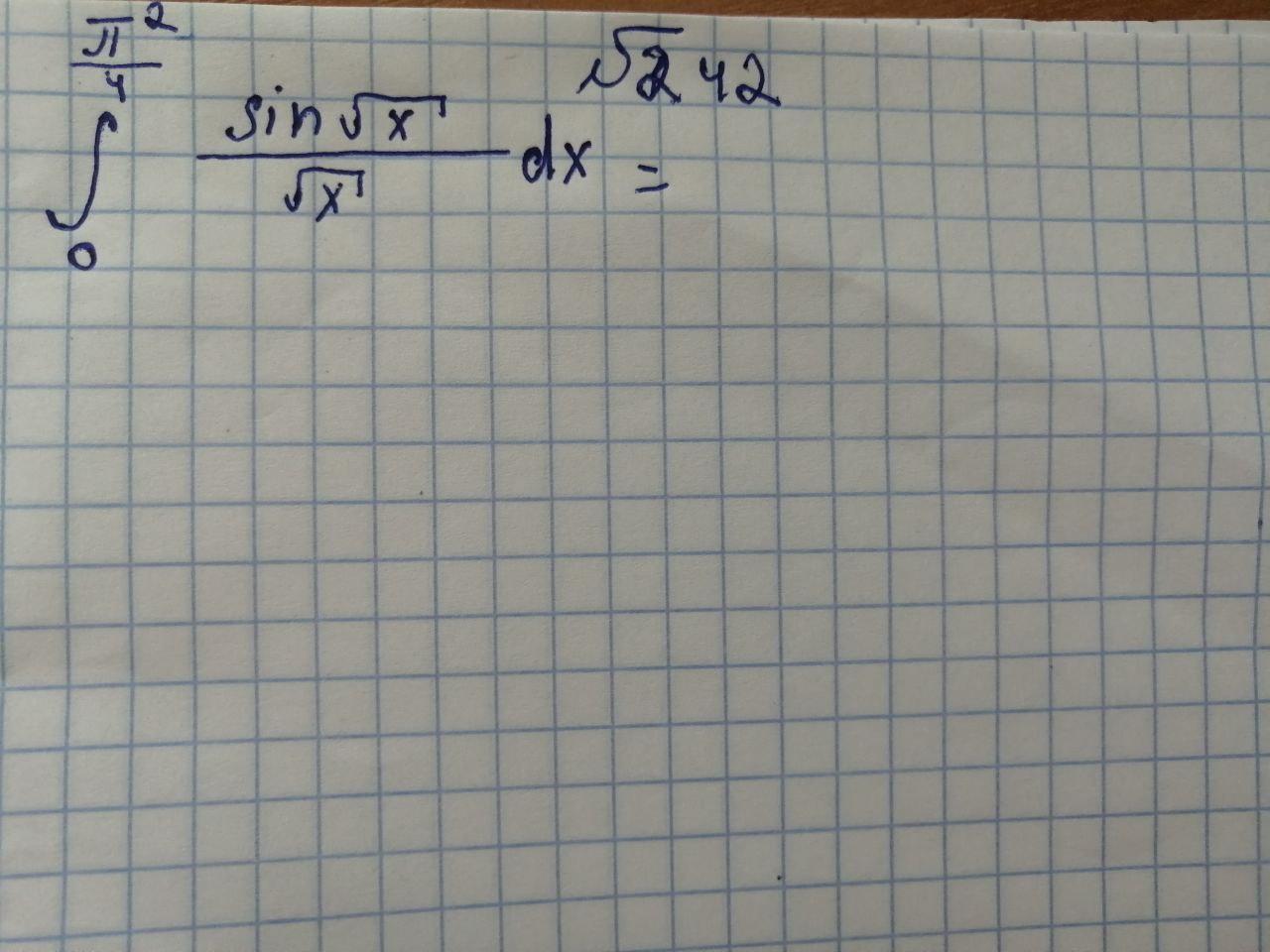
mathgenius:
-2cos(sqrt(pi^2/4)) +2cos(0)= 2-2cos(pi/2) =2
Неопр. ин-т: -2cos(sqrt(x)) +c
Ответы
Ответ дал:
2
Объяснение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад