Question

Докажите, что прямая, перпендикулярная бисектрисе угла, разделяет на его сторонах одинаковые отрезки (ответ полный)

Answer 1

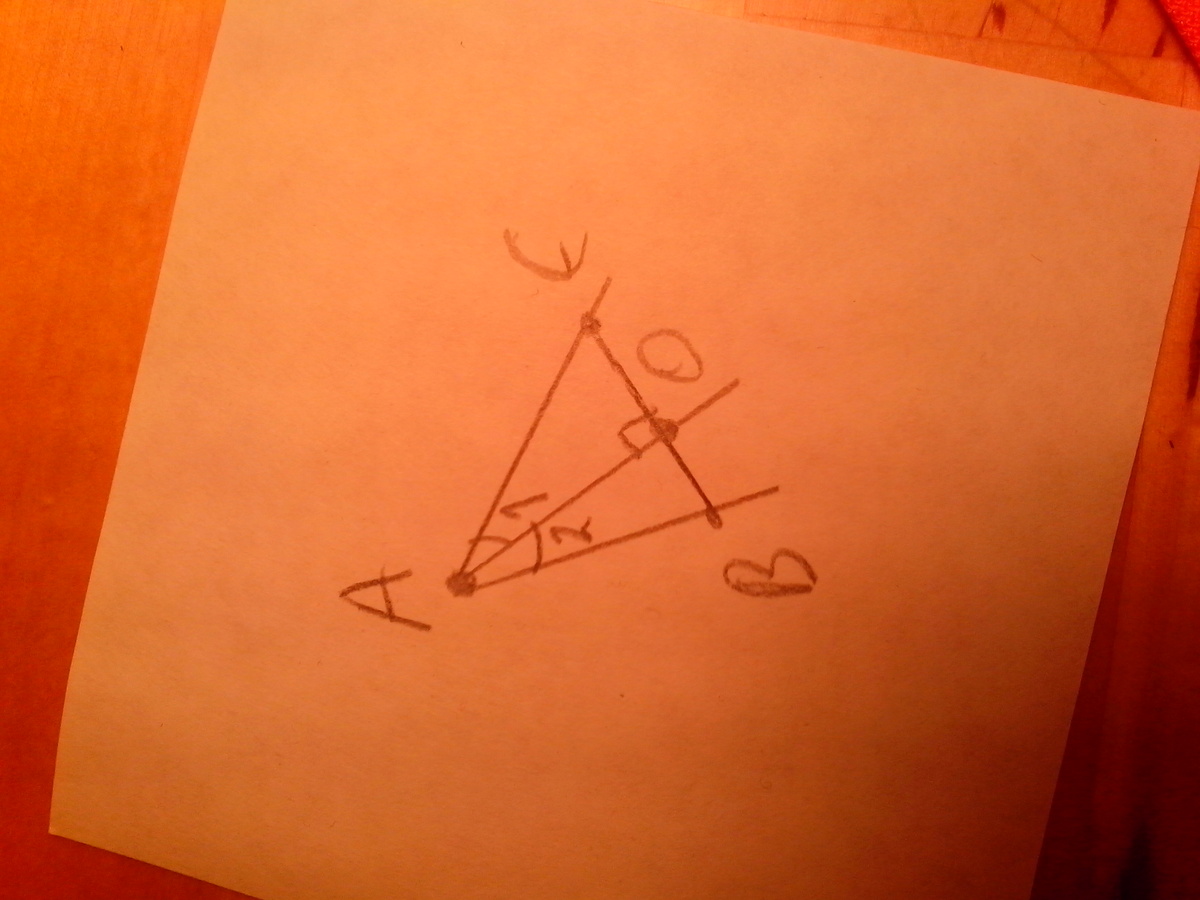
Дано: угол А, прямая АО - биссектрисса угла А. прямая ВС перпендикулярна АО, точки В и С - лежат на сторонах угла. Доказать: АС=АВ.
Рассмотрим 2 прямоугольных треугольник: АВО и АСО. (они прямоуголльные т.к. ВС перпендикулярна АО):
             АО - общий катет
             угол 1=углу 2 (т.к. АО - биссектрисса)
           Значит треугольник АВО=треугольнику АСО по катету и острому углу. Из этого следует что АВ=АС что и требовалось доказать.