Помогите пожалуйста,очень надо!
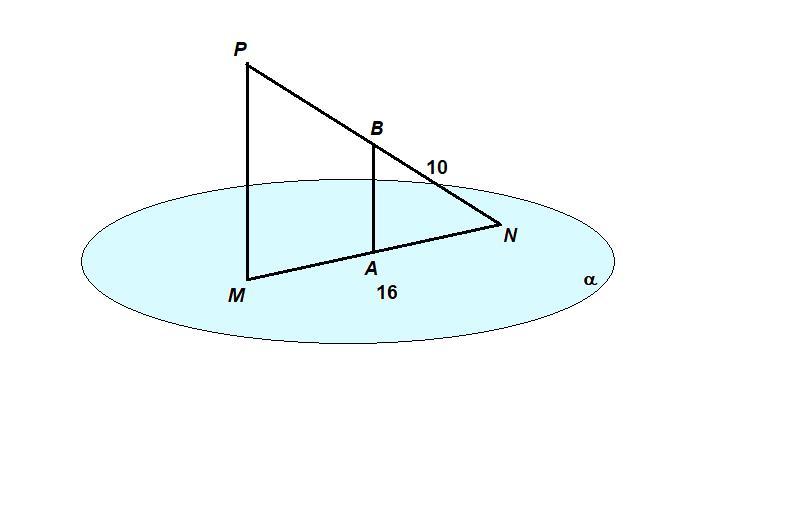
Точки М и N лежат,а точка Р не лежит в плоскости а.Точки А и В середины отрезка MN и NP ,АВ перпендикулярна а,MN=16 ,BN=10.Найдите расстояние от точки Р до плоскости а.
Приложения:

Ответы
Ответ дал:
0
точки В и А середины отрезков ВА перпедикулярно плоскости следовательно РМ паралельна ВА и также перпедикулярна плоскости. следовательно расстояние от Р до плоскости = РМ, следовательно имеем прямоугольный треугольник в котором PN = 20, MN = 16, по теореме Пифагора PM= корень из(20^2-16^2)=корень из144=12
Ответ дал:
0
Ответ: 12
Пошаговое объяснение:
АВ - средняя линия треугольника MNP, значит PM ║ AB.
АВ ⊥ α, значит и РМ ⊥ α.
РМ - искомое расстояние.
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в плоскости, значит
РМ ⊥ MN.
PN = 2BN = 20.
ΔPMN: ∠PMN = 90°, по теореме Пифагора
PM = √(PN² - MN²) = √(400 - 256) = √144 = 12
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад