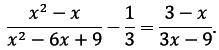Ответы
Ответ дал:
0
Ответ:
Объяснение:
Смотри вложение
Приложения:

Ответ дал:
0
Ответ:
Корнями уравнения являются числа: 0 и 1.
Объяснение:
Данное уравнение равносильно следующей системе:
{x(x - 1) = 0, {x = 0; x - 1 = 0, {x₁ = 0; x₂ = 1,
{(x - 3)² ≠ 0 <=> {x ≠ 3 <=> {x ≠ 3
Ответ: 0; 1.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад