Question

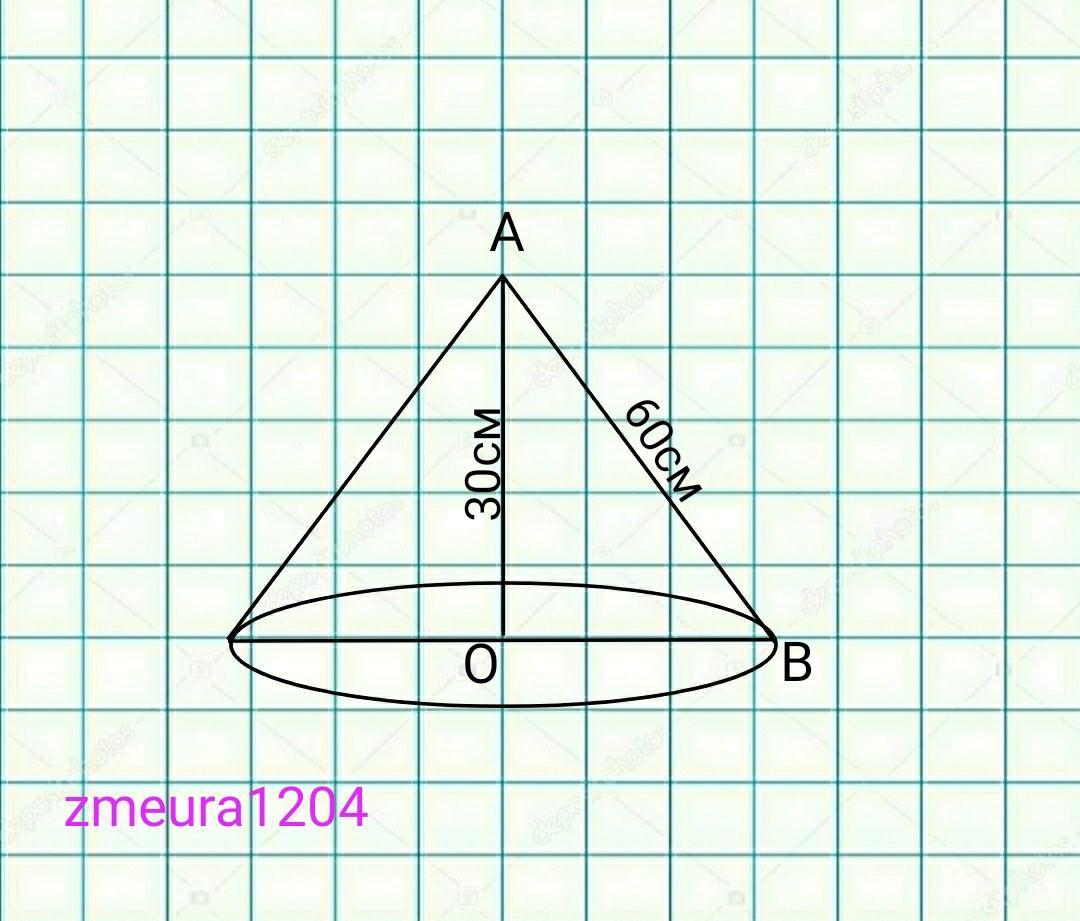
Образующая конуса равна 60 см, высота 30 см. Найдите площадь боковой поверхности конуса. Решите все 3 задания - дам 80 баллов. Мне очень срочно надо

Answer 1

Ответ:

Объяснение:

1)

Теорема Пифагора

ОВ=√(АВ²-АО²)=√(60²-30²)=30√3 см. радиус окружности

Sбок=πRL, где R=30√3см; L=60см

Sбок=30√3*60*π=1800π√3см²

Ответ: 1800π√3см²

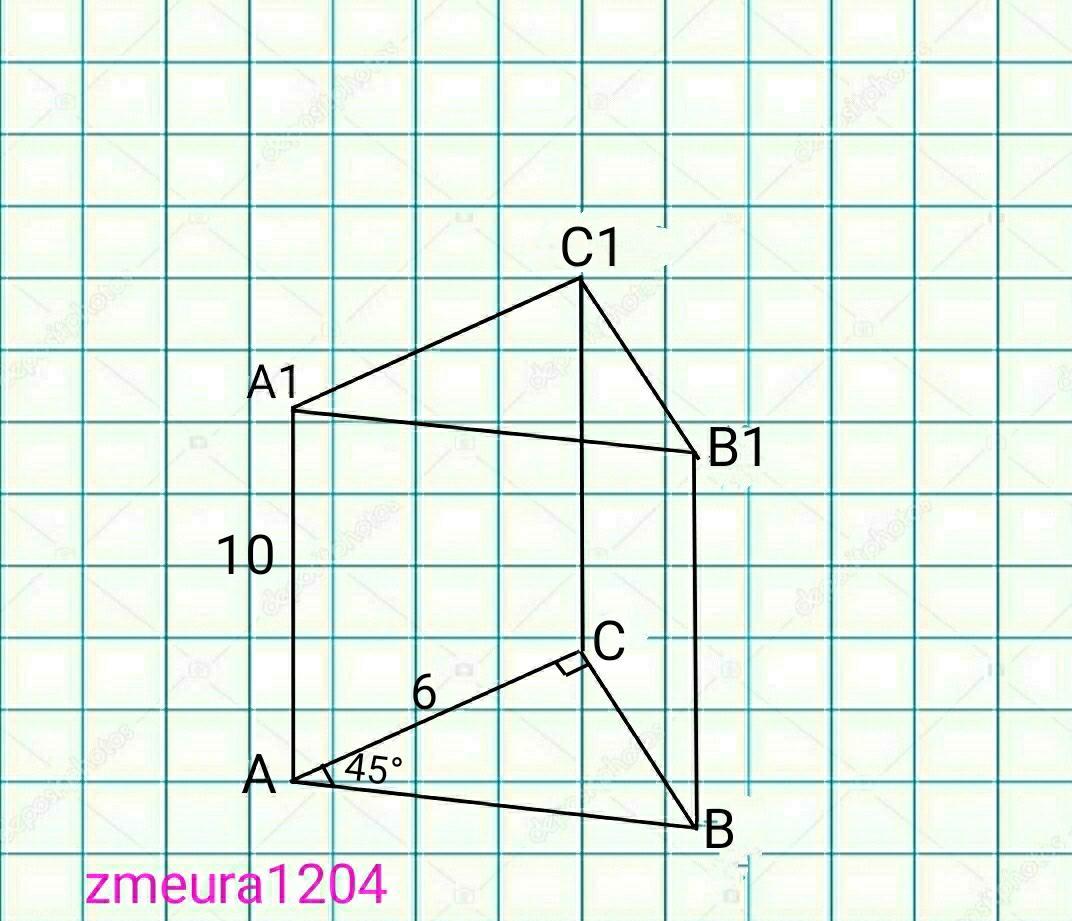
2)

∆АВС- равнобедренный треугольник (углы при основании равны по 45°)

АС=СВ=6см.

Sосн=1/2*АС*СВ=1/2*6*6=18см²

Теорема Пифагора

АВ=√(АС²+СВ²)=√(6²+6²)=6√2см.

Росн=АС+СВ+АВ=6+6+6√2=12+6√2см.

Sбок=Росн*АА1=10(12+6√2)=120+60√2см²

Sпол=Sбок+2Sосн=2*18+120+60√2=

=156+60√2см²

Ответ: 156+60√2см²

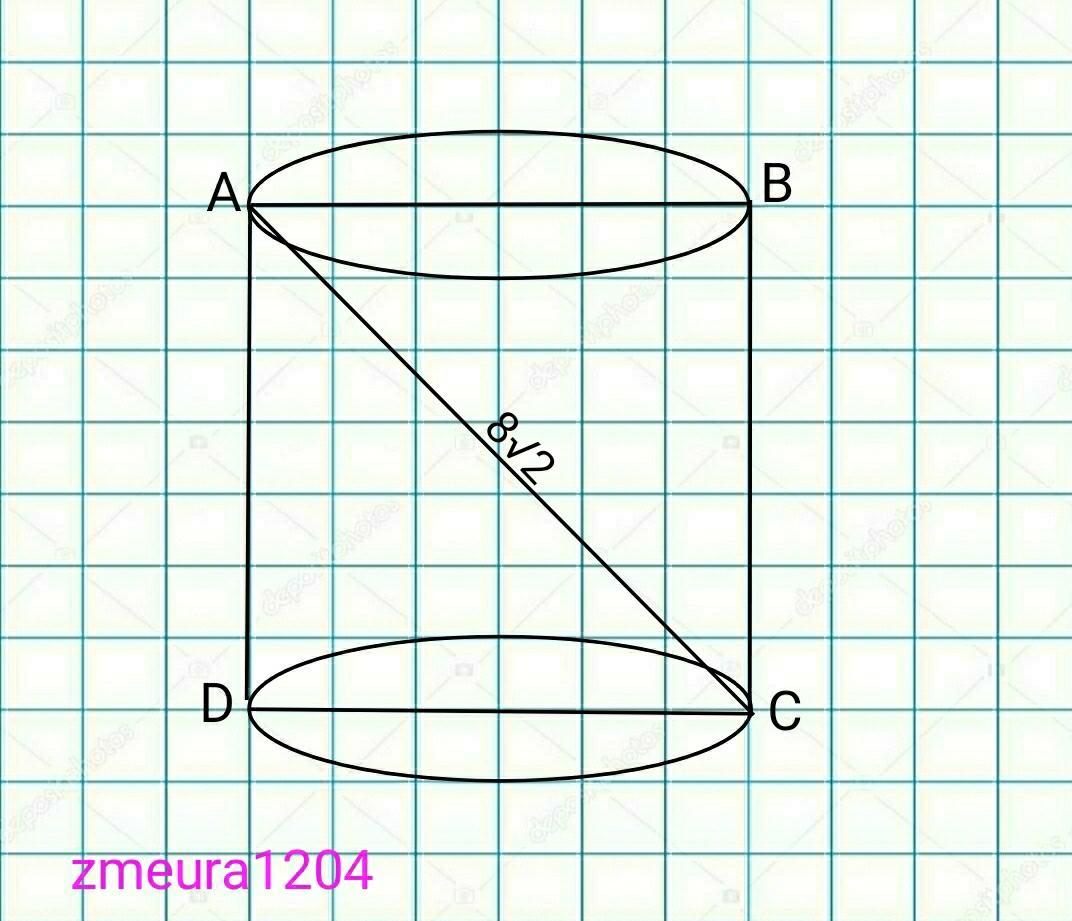
3)

АD=DC, по условию

АD=AC/√2=8√2/√2=8см

DC=8см

С=πD=π*DC=8π см длина окружности основания

Sбок=С*АD=8π*8=64π см²

Ответ: 64π см²