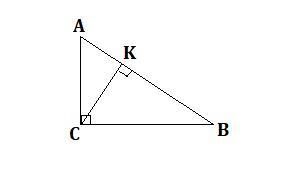
высота CK прямоугольного треугольника АВС, проведенная к гипотенузе , делит ее на отрезки длиной 8 см и 32 см . найдите катеты и периметр треугольника
Ответы
Ответ дал:
1
Ответ:
см,
см,
см или
см
Пошаговое объяснение:
AK = 8 см, BK = 32 см
- Катеты прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
То есть:
см
см
см
см
Приложения:
Аноним:
можете пж решить там таакже ток цывры другие 12 и 27
Вас заинтересует
3 года назад
8 лет назад