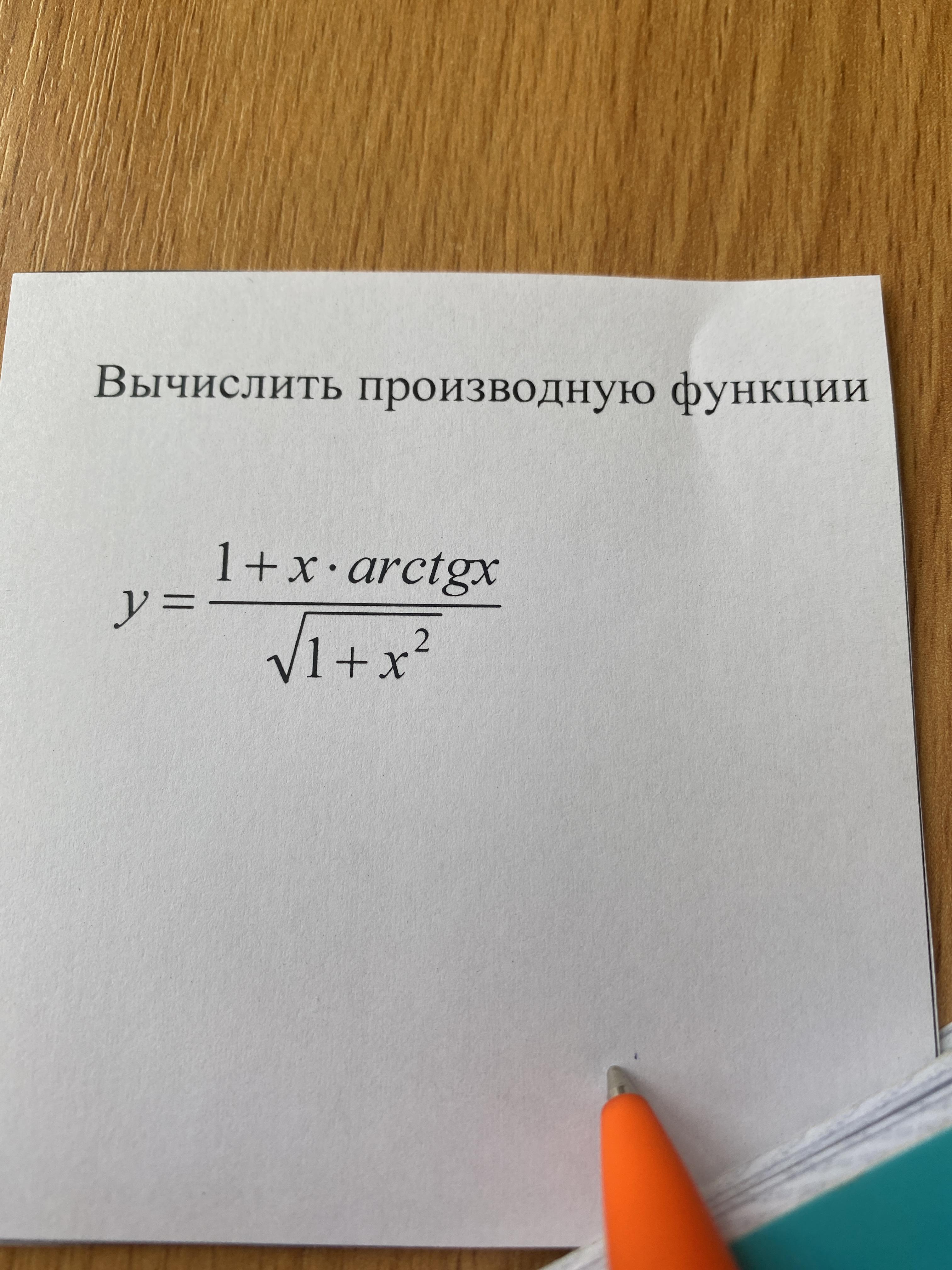Ответы
Ответ дал:
0
(u/v)'=(u'v-uv')/v²; здесь u=1+x*arctgx; v=√(1+x²);
(xy)'=x'y+xy'
(const)'=0;
(√u)'=(1/(2√u))*u'
x'=1;
(arctgx)'=1/(1+x²);
y'=((arctgx+(x/(1+x²)))*(√(1+x²))-(1+x*arctgx)*(2x/(2√(1+x²)))/(1+x²)=
((arctgx+(x/(1+x²)))*(√(1+x²))-(1+x*arctgx)*(x/(√(1+x²)))/(1+x²)
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
10 лет назад