Ответы
Ответ дал:
1
Ответ: S=156 .
Ответ дал:
0
Ответ:
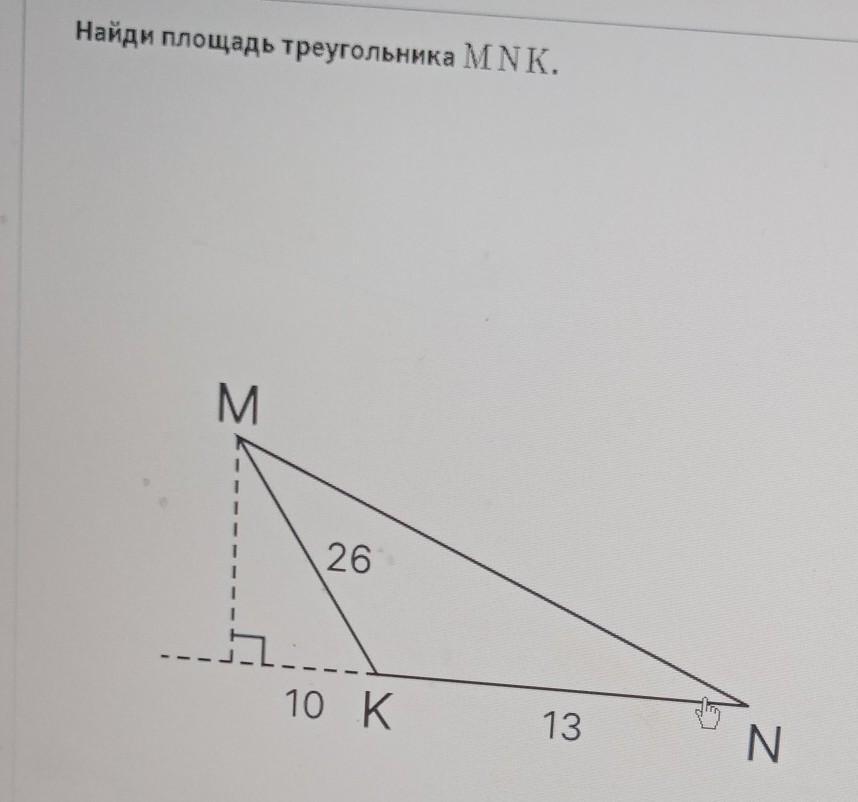
отметим точку, например, О так, чтобы МО являлась высотой треугольника MKN.
Заметим, что треугольник МКО прямоугольный и мы знаем один катет ОК=10 и гипотенузу МК=26
Найдем МО
площадь треугольника равна половине высоты на, основание треугольника, к которому проведена эта высота
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад