Дан треугольник ABC, его площадь (S), радиус вписанной окружности (r) и угол A. Найти сторону BC.
Ответы
Ответ дал:
1
Дан треугольник ABC, его площадь (S), радиус вписанной окружности (r) и угол A. Найти сторону BC.
Если есть площадь треугольника и радиус вписанной окружности, то находим значение полупериметра р.
p = S/r.
В величину полупериметра входит одна сторона полностью и отрезок другой стороны от вершины до точки касания с вписанной окружностью.
Этот отрезок равен r/(tg(A/2)).
Ответ: BC = (S/r) - (r/(tg(A/2))).
Можно проверить на конкретном примере.
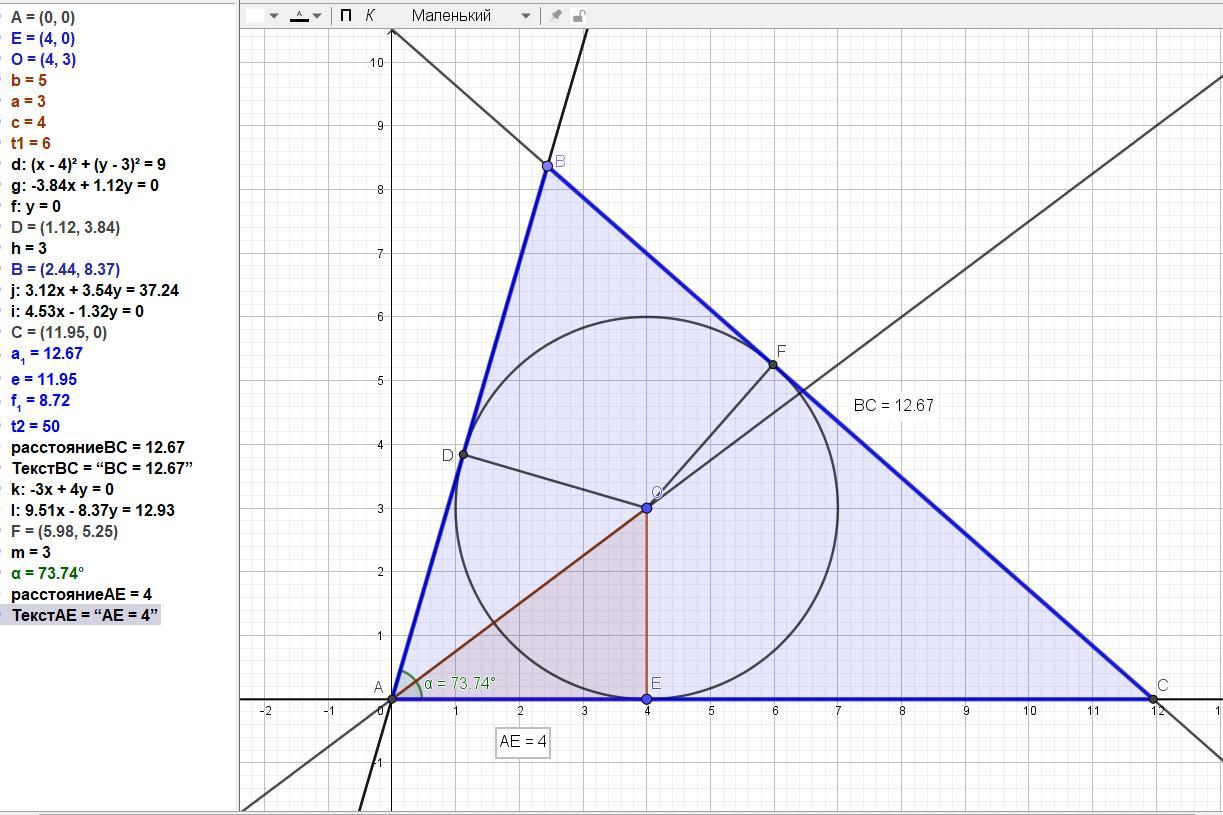
Пусть дан треугольник с площадью 50 кв. ед., угол, тангенс половины которого равен 3/4 и вписанная окружность радиусом 3.
Получаем ВС = (50/3) - ( = 3/(3/4)) = (50/3) - 4 = 12,67.
Проверка произведена с помощью графического редактора GeoGebra и результат подтверждён: ВС = 12,67.
Приложения:
Akakiynas845:
Не могли бы вы объяснить, как выразили эту формулу, а опишите пожалуйста точнее это решение
Надо разобраться со свойством полупериметра. В тексте ответа об этом говорится.
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад