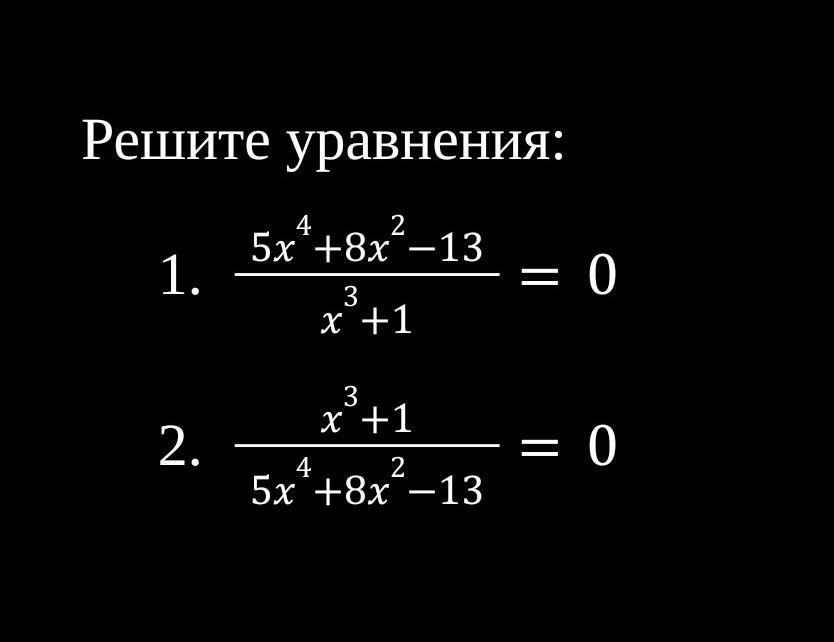Question

Помогите исправить оценку пожалуйста ​

Answer 1

$1) \frac{5x {}^{4} + 8x {}^{2} + 13}{x {}^{3} + 1} = 0 \: \: x≠ - 1 \\ 5x {}^{4} + 8x {}^{2} + 13 = 0 \\ x∉ℝ$

если левая часть положительная то утверждение ложно

$2) \frac{x {}^{3} + 1 }{5x {}^{4} + 8x {}^{2} - 13 } = 0 \\ \\ \frac{(x + 1) \times (x {}^{2} - x \times 1) }{(5x {}^{2} + 13)(x - 1)(x + 1) } = 0 \\ x {}^{2} - x + 1 = 0 \\ \\ x = \frac{ - ( - 1)± \sqrt{( - 1) {}^{2} - 4 \times 1 \times 1 } }{2 \times 1} \\ \\ x = \frac{1± \sqrt{1 - 4} }{2} \\ \\ x = \frac{1± \sqrt{ - 3} }{2}$

x ∉ℝ

тоже самое как с первым

Answer 2

(5x⁴ + 8x² - 13)/(x³ + 1) = 0

одз x³ + 1 ≠ 0

(x + 1)(x² - x + 1) = 0

x ≠ -1

5x⁴ + 8x² - 13 = 0

x² = y ≥ 0

5y² + 8y - 13 = 0

D = 64 + 260 = 324

y12 = (-8 +- 18)/10 = - 26/10   1

y1 = -26/10 < 0 нет

y2 = 1

x² = 1

x1 = -1 нет по одз

x2 = 1

отвЕт х = 1

=====

(x³ + 1)/(5x⁴ + 8x² - 13) = 0

одз 5x⁴ + 8x² - 13 ≠ 0

x ≠ {-1, 1}

x³ + 1 = 0

x = -1 нет по одз

решений нет