Question

помогите пожалуйста ​

Answer 1

Ответ:

∠ДНС=30°

Объяснение:

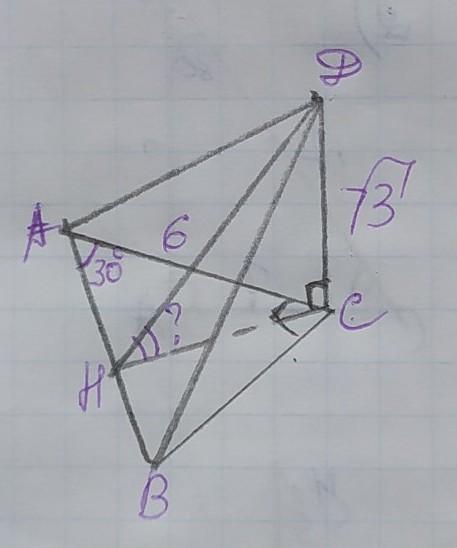
Проведём два перпендикуляра ДН и СН к стороне АВ. ∠ДНС между этими прямыми – это угол между плоскостями, который нужно будет найти. СН делит ∆АВС на 2 прямоугольных треугольника АСН и СВН. Рассмотрим ∆АСН. У него АН и СН – катеты, а АС – гипотенуза. Из ∆АСН найдём СН через синус угла. Синус угла – это отношение противолежащего от угла катета к гипотенузе, поэтому:

$\\ \\ \sin(a) = \frac{ch}{ac}$

Отсюда: CH=AC×sinA=6×sin30°=6×1/2=3; CH=3.

Рассмотрим ∆ДНС. Он прямоугольный, ДС и СН – катеты, а ДН – гипотенуза. Из ∆ДНС найдём ∠ДНС через тангенс угла.

Тангенс – это отношение противолежащего от угла катета к прилежащему, поэтому:

$\\ \\ \tan(dhc) = \frac{dc}{ch} = \frac{ \sqrt{3} }{3} = 30$

∠ДНС=30°