Question

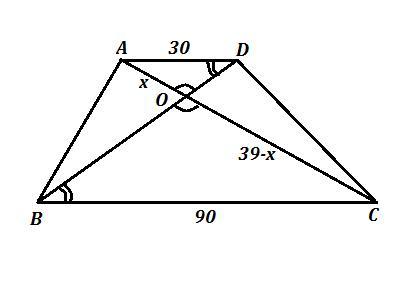
у трапеції abcd ad || bc, o - точка перетину діагоналей, знайти oc, якщо bc=90, ad=30, ac=39
пж, срочно ❤️❤️❤️❤️​

Answer 1

треугольники АОD и СОВ подобны по первому признаку подобия. у них ∠АОD=∠СОВ, как вертикальные, ∠ОАD=∠ОСВ как внутренние накрест лежащие при АD║ВС и секущей АС, если обозначить ОС=х, то АО=39-х

составим пропорцию, вытекающую из подобия треугольников.

АО/СО=АД/ВС; х/(39-х)=90/30; 90*(39-х)=30*х; 3*39-3х=х; 4х=3*39;х=3*39/4=29.25

Ответ 29.25

Answer 2

Ответ:   ОС=29,25 .

ABCD - трапеция, АD || ВС , АD=30 ,  ВС=90 ,  АС=39 ,

точка О - точка пересечения диагоналей .

Обозначим ОА=х , тогда  ОС=39-х .

ΔАОD ~ ΔВОС , по двум углам ( ∠АОD=∠ВОС как вертикальные ,

∠АDB=∠CВD как внутренние накрест лежащие углы при параллельных АD и ВС и секущей АС .

Из подобия треугольников следует пропорциональность соответствующих сторон.

$\dfrac{BC}{AD}=\dfrac{OC}{OA}\ \ \Rightarrow \ \ \ \dfrac{90}{30}=\dfrac{39-x}{x}\ \ ,\ \ \ \dfrac{39-x}{x}=3\ \ ,\ \ 39-x=3x\ \ ,\\\\\\39=4x\ \ ,\ \ \ x=9,75\ \ ,\ \ \ 39-x=29,25$