Question

mabcd правильная пирамида ad=am=2 найдите угол de bm​

Answer 1

Ответ:

$\boxed{\angle(DE, BM) = \arccos \left (\dfrac{\sqrt{12} }{12} \right) }$

Объяснение:

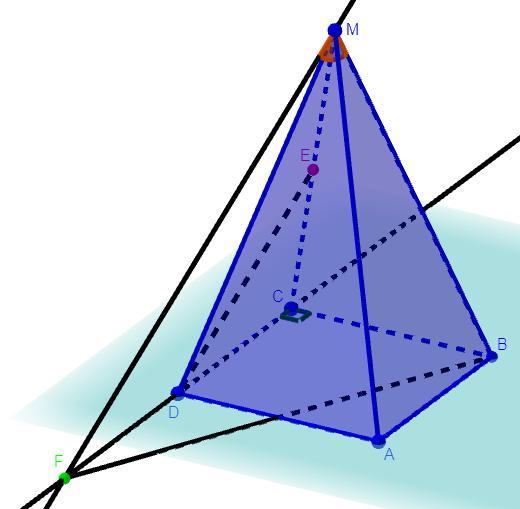
Дано: MABCD - правильная пирамида, AD = AM = 2, ME = EC

Найти: ∠(DE, BM) - ?

Решение: Так как по условию MABCD - правильная пирамида, то по определению правильной пирамиды в её основании лежит правильный многоугольник. Так как согласно рисунку пирамида - четырехугольная, то в основании лежит правильный четырехугольник, то есть квадрат, следовательно ABCD - квадрат. По свойствам квадрата (ABCD) все его стороны равны, тогда AD = AB = BC = DC = 2. Так как пирамиды правильная, то её грани являются равными равнобедренными треугольниками по свойствам правильной пирамиды (где боковые ребра равные стороны). Так как по условию AD = AM = 2, то основание равнобедренного треугольника равно его боковой стороне, тогда по теореме данный треугольник правильный, а так как все треугольники равны, то боковые грани пирамиды являются правильными треугольниками и все ребра пирамиды равны между собой, то есть AD = AB = BC = DC = MA = MB = MC = MD = 2. Через точку M проведем прямую параллельную DE. Так как прямая DE пересекает прямую CD, то и прямая проходящая через точку M и параллельная DE также пересекает прямую CD. Пусть прямая проходящая через точку M и параллельная DE пересекает прямую CD в точке F. Так как MF║DE, то прямые лежат в одной плоскости по теореме. Так как MF║DE и по условию ME = EC, то по теореме Фалеса FD = DC. По основному свойства отрезка: FC = FD + DC = 2FD = 2DC =

= 2 * 2 = 4. Так как ABCD - квадрат, то по свойствам квадрата все его углы равны 90°, следовательно угол ∠DCB = 90°, тогда треугольник ΔFCB - прямоугольный. По теореме Пифагора для треугольника ΔFCB:$FB = \sqrt{FC^{2} + FB^{2}} = \sqrt{4^{2} + 2^{2}} = \sqrt{16 + 4} = \sqrt{20}$. Рассмотрим треугольник ΔMDC. Так как треугольник ΔMDC - правильный, то по свойствам правильного треугольника все его углы равны 60°, тогда угол

∠DCM = 60°. Так как точка M - середина отрезка MC, то DE - медиана правильного треугольника ΔMDC, а по теореме медиана в правильном треугольнике является биссектрисой и высотой. Площадь треугольника ΔMDC: $\displaystyle \left \{ {{S_{зMDC} = 0,5 \cdot DC \cdot MC \cdot \sin \angle DCM} \atop {S_{зMDC} = 0,5 \cdot DE \cdot MC}} \right \Longrightarrow$

$0,5 \cdot DC \cdot MC \cdot \sin \angle DCM =0,5 \cdot DE \cdot MC|:(0,5\cdot MC)$

$DE = MC \cdot \sin \angle DCM = 2 \cdot \sin 60^{\circ} = 2 \cdot \dfrac{\sqrt{3} }{2} = \sqrt{3}$.

Рассмотрим треугольник ΔFMC. Так как MF║DE и ME = EC, FD = DC, то отрезок DE - средняя линия по определению. По свойству средней линии: $FM = 2DE = 2\sqrt{3} = \sqrt{4 \cdot 3} = \sqrt{12}$. Рассмотрим треугольник ΔFMB. По теореме косинусов:$FB^{2} = MF^{2} + MB^{2} - 2 \cdot MF \cdot MB \cdot \cos \angle FMB \Longrightarrow$

$\Longrightarrow \cos \angle FMB= \dfrac{ MF^{2} + MB^{2} - FB^{2} }{2 \cdot MF \cdot MB} = \dfrac{ (\sqrt{12} )^{2} + 2^{2} - (\sqrt{20} )^{2} }{2 \cdot \sqrt{12} \cdot 2} =$

$= \dfrac{12 + 4 - 20}{4\sqrt{12} } =-\dfrac{4}{4\sqrt{12} } = -\dfrac{1}{\sqrt{12} } = -\dfrac{1 \cdot \sqrt{12} }{\sqrt{12} \cdot \sqrt{12} } = -\dfrac{\sqrt{12} }{12}$.

Так как прямые DE и MB - скрещивающиеся, то по определению угол между скрещивающимися прямыми это угол между прямыми которые пересекаются и соответственно параллельны данным скрещивающимся прямым, так как MF║DE, то угол между прямыми DE и MB равен углу между прямыми MF и DE, то есть

∠(DE, BM) = ∠(FM, BM). По определению угол между прямыми принадлежит промежутку от 0° до 90° включительно. При пересечение прямых образуются два угла. Так как угол ∠FMB - это угол который образуется при пересечении прямых FM и MB. Так как cos ∠FMB < 0, то угол ∠FMB > 90°, то есть нужно найти косинус угла смежного с углом ∠FMB. Угол смежный с углом ∠FMB равен (180° - ∠FMB), так как сумма смежных углов 180°. Так как угол ∠FMB > 90°, то угол

(180° - ∠FMB) < 90°.

cos (180° - ∠FMB) = - cos ∠FMB = $\dfrac{\sqrt{12} }{12}$. Тогда:

$\angle(DE, BM) = \arccos \left (\dfrac{\sqrt{12} }{12} \right)$.