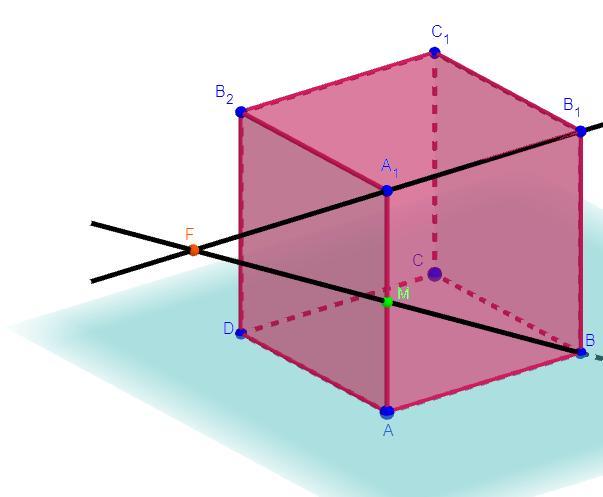
Дан куб ABCDA1B1C1D1. Точка М – середина ребра АА1. Построить точку пересечения прямой МВ с площадью A1B1C1.
Ответы
Ответ дал:
1
Ответ:
План построения!
Объяснение:
Дано: ,
Построить:
План построения: Проведем прямые и
. Так как по условию
, а
, то
. Так как
, то по аксиоме стереометрии
.Так как
, то по аксиоме стереометрии
. Так как
и
, то
. Пусть
.Так как
, то по аксиоме стереометрии
. Так как
, а
, то
.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад