Помогите с алгеброй!
Приложения:
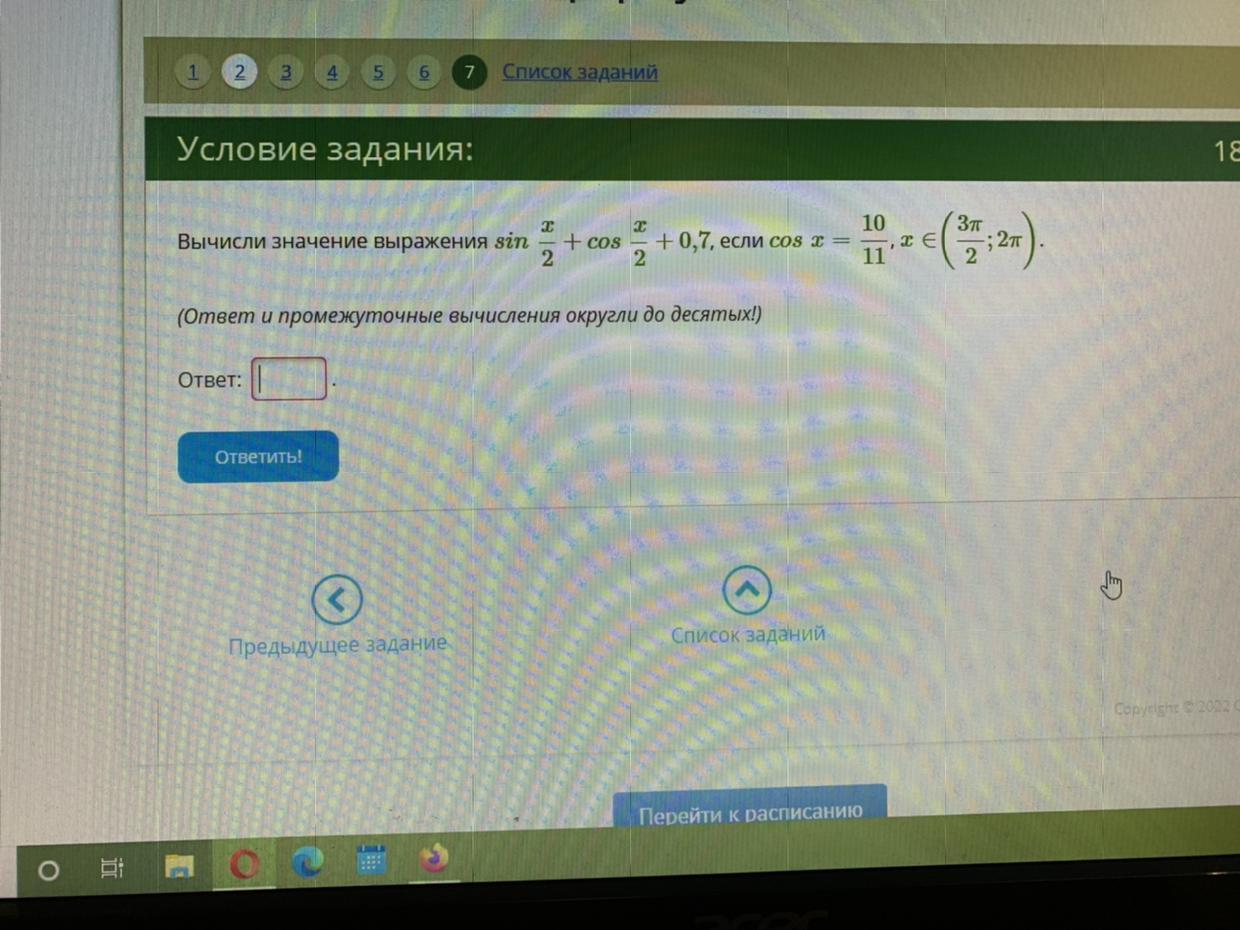
margaritakiseleva:
у меня получилось 1,46. Но я абсолютно не уверена
Напоминает формулу, но не могу вспомнить
1.9
Ответы
Ответ дал:
0
Формулы синуса и косинуса половинного угла выглядят так:
_______________________
Чтобы определить знак перед корнем, нужно понять, в какой четверти лежит этот угол.
По условию:
Преобразуем неравенство, разделив все его части на 2:
То есть угол лежит во второй четверти.
Значит, синус этого угла положительный, а косинус — отрицательный (см. вложение).
Теперь можем использовать формулы:
По условию, . Подставляем это значение в выражение:
Ответ: - 0,1.
Приложения:
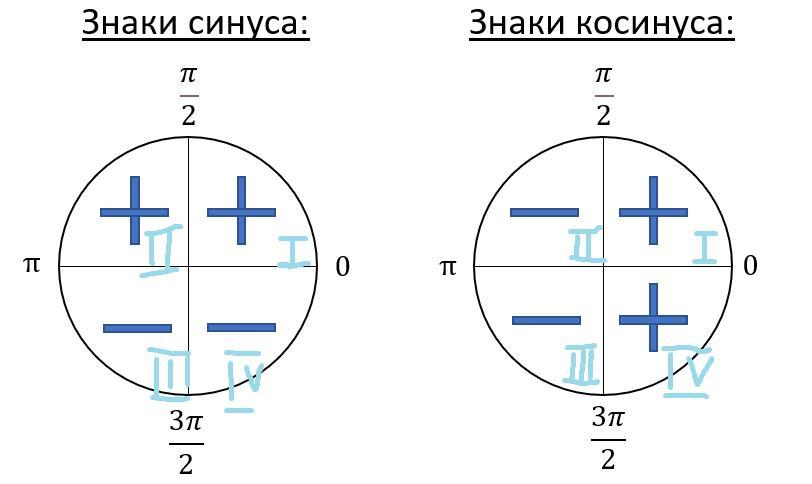
Какие знаки косиуса и синуса х/2?
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад