Продолжите ряд чисел
Приложения:
ВикаБач:
У таких задач может быть много решений, слишком мало чисел дано. Одно из решений: первые разности 10;24;44;70... вторые разности 14;20;26... третьи разности 6;6....ПРЕДПОЛОЖИМ, что ряд чисел построен таким образом, что третьи разности одинаковые и равны 6. В этом случае продолжение ряда будет ...252, 392, 576... (Повторюсь, это решение может не совпасть с авторским решением, НО это тоже решение).
на держи
отметь мой ответ лучшим, пж
Задача имеет вполне конкретное решение. Решение и ответ готовы.
Vasily1975, понятно, что если третьи разности - постоянное число, то формула общего члена - многочлен 3 степени от номера, но в задании не требовалось найти эту формулу, а просто продолжить этот ряд, что можно сделать и не зная её, а пользуясь рекуррентными соотношениями, ну и всё же, это одно из возможных продолжений этой достаточно короткой последовательности....
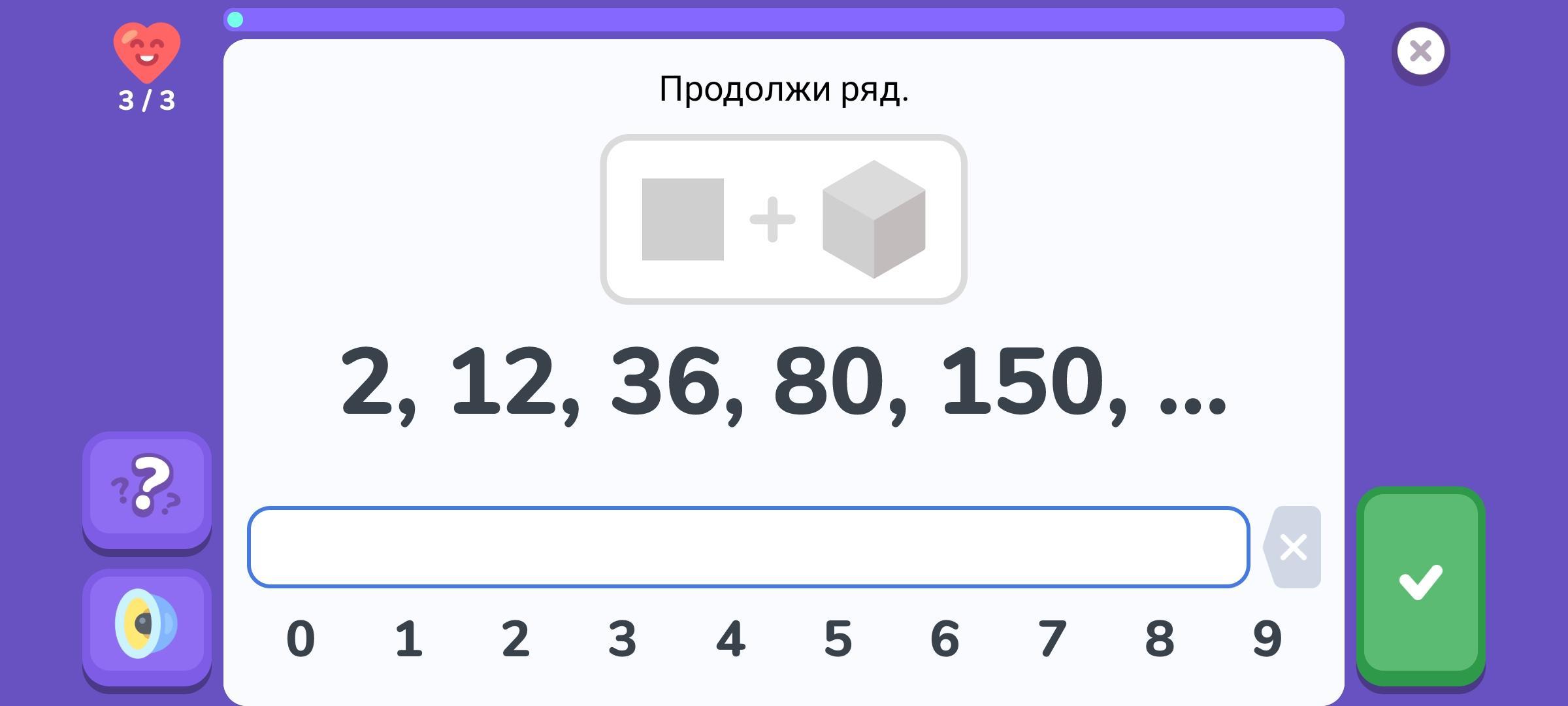
Да, и в задании есть явная подсказка на рисунке "квадрат+куб", а если бы её не было?
Я и не обратил внимание на эту "подсказку".
Ответы
Ответ дал:
0
Ответ: a6=252 и.т.д. по формуле an=n²*(n+1).
Пошаговое объяснение:
Пусть n - порядковый номер члена ряда. Замечаем, что a1=1²*2=2, a2=2²*3=12, a3=3²*4=36, a4=4²*5=80, a5=5²*6=150. Отсюда ясно, что общий член ряда an=n²*(n+1). Поэтому следующим числом будет a6=6²*7=252, и.т.д.
Ответ дал:
0
Ответ: 252; 392; 576...
Пошаговое объяснение:
общая формула, по которой можно найти последующие члены
х²+х³
проверяем
х=1; 1²+1³=2
х=2; 2²+2³=4+8=12
х=3; 3²+3³=9+27=36
х=4; 4²+4³=16+64=80
х=5; 5²+5³=25+125=150
х=6; 6²+6³ =36+216=252
х=7; 7²+7³=49+343=392
х=8; 8²+8³ =64+512=576
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад