Помогите, пожалуйста, найти предел последовательности при n, стремящемся к бесконечности
Приложения:
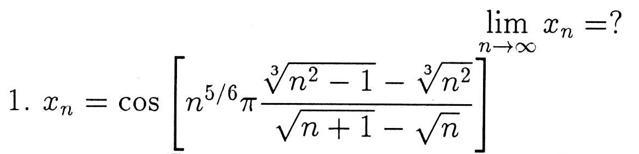
Ответы
Ответ дал:
1
Будем пользоваться непрерывностью косинуса, тем самым обосновывая справедливость внесения знака предела под аргумент.
, это получилось умножением числителя и знаменателя на сопряженное. Раскрываем скобки:
. Вынесем
:
. Разложим каждую скобку по формуле Тейлора в окрестности
с точностью до квадратичных членов:
После раскрытия скобок получим . Значит,
.
zajnullinnail52:
Спасибо большое
а можете пожалуйста объяснить, как вы разложили скобки по Тейлору? у меня там получается бесконечность в вычислении производных в точке х0=0
а зачем производные вычислять? есть же формула для (1+x)^a
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад