Question

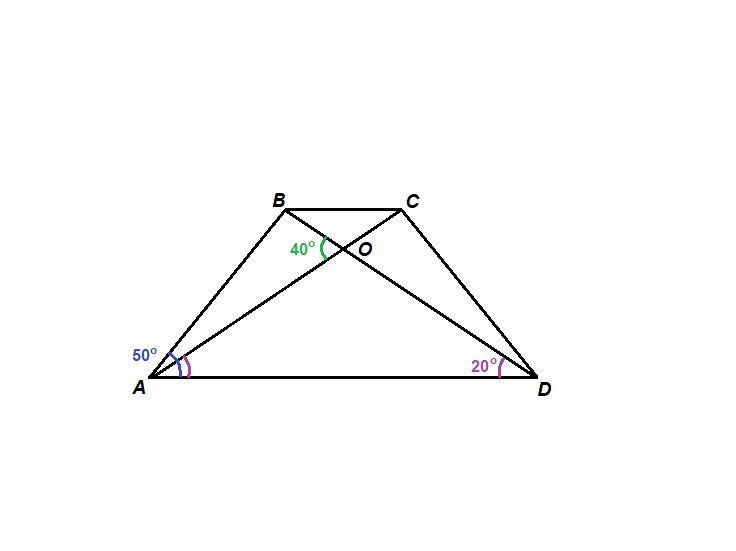
У трапеції кут при більшій основі дорівнкюе 50°, а менший кут між діагоналями дорівнюе 40°. Де лежить центр кола, описаного навколо трапеції, — всередині трапеції чи поза нею? Відповідь обрунтуйте.​

Answer 1

Ответ:

Центр окружности, описанной около данной трапеции, лежит вне трапеции.

Объяснение:

• Если окружность описана около трапеции, то трапеция равнобедренная.

Рассмотрим треугольники ADB и DAC:

• АВ = CD, так как трапеция равнобедренная,
• ∠BAD = ∠CDA как углы при основании равнобедренной трапеции,
• AD - общая сторона, значит

ΔADB = ΔDAC по двум сторонам и углу между ними.

Из равенства треугольников следует, что

∠BDA = ∠CAD или иначе ∠ОDA = ∠ОAD.

• Внешний угол треугольника равен двум внутренним, не смежным с ним.

∠ВОА = ∠OAD + ∠ODA (внешний для ΔODA)

∠OAD = ∠ODA = ∠ВОА : 2 = 40° : 2 = 20°

В треугольнике ABD

∠ABD = 180° - (∠BAD + ∠BDA) = 180° - (50° + 20°) = 180° - 70° = 110°

• Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.

ΔABD вписан в ту же окружность, что и трапеция.

Значит, центр окружности, описанной около данной трапеции, лежит вне трапеции.