Question

СРОЧНО ПОМОГИТЕ С ДЗ!

1.Вычисли периметр ромба, если длина одной его стороны равна 4,53 м
(в окошке запиши только число).
Периметр равен м.

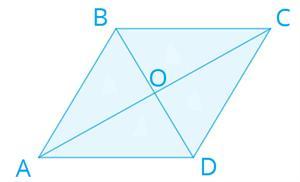
2.Дано: BO = 9 см;
AC= 8 см.
Найти: BD; OA.
Ответ:
BD= см;
OA = см.

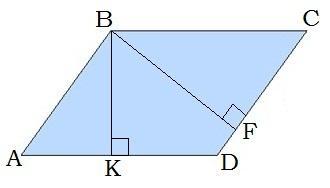
3.Дано:
CD= 12 см;
AD= 10 см;
BF=5 см;
Найти: S(ABCD).
Ответ:площадь параллелограмма ABCD равна см2.

Answer 1

Ответ:

1. Р = 18,12 (м²)

2. BD = 18 см, OA = 4 см.

3. S = 60 см²

Объяснение:

• 1. Периметр - сумма длин всех сторон ромба.

Так как у ромба все стороны равны, то его периметр можно рассчитать по формуле:

Р = 4а , где а - сторона ромба.

⇒ Р = 4,53 · 4 = 18,12 (м²)

2. В параллелограмме ABCD ВD и АС - диагонали.

• Диагонали параллелограмма точкой пересечения делятся пополам;

⇒ ВО = ОD = 9 см   ⇒ BD = 9 + 9 = 18 (см);

АС = 8 см  ⇒ ОА = ОС = 8 : 2 = 4 (см)

3.

• Площадь параллелограмма равна произведению основания на высоту.

За основание принимаем ту сторону, к которой проведена высота.

То есть:

S = AD * BK    или    S = DС * BF

Нам известны DC = 12 см и  BF = 5 см. Поэтому воспользуемся второй формулой.

S = 12 * 5 = 60 (см²)