Question

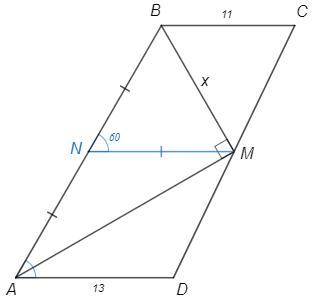
В трапеции ABCD боковая сторона AB видна из середины M стороны CD под прямым углом. Найдите длину BM, если AD=13, BC=11, ∠A=60∘

Answer 1

N - середина AB.

NM - средняя линия трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

NM||AD => ∠BNM=∠BAD=60° (соответственные углы при параллельных)

NM=(AD+BC)/2 =(13+11)/2 =12

NM - медиана в прямоугольном треугольнике ABM.

Медиана из прямого угла равна половине гипотенузы.

NM=AB/2=NB

△BNM - равнобедренный с углом 60° => равносторонний.

BM=NM=12