Question

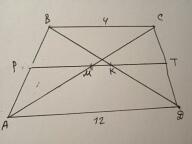
2. Діагоналі AC i BD трапеції ABCD (BC || AD) перетинають середню лінію трапеції в точках M iK відповідно. Відомо, що BC = 4 см, AD = 12 см. Знайдіть відрізок МК.​

Answer 1

Ответ:

4 см.

Объяснение:

Проведемо РТ - середню лінію.

Середня лінія трапеції дорівнює напівсумі основ.

РТ=(4+12):2=8 см.

Розглянемо ΔАВD. РК - середня лінія, РК=1/2 АD=12:2=6 см.

Розглянемо ΔАСD. MТ - середня лінія,  МТ=1/2 АD=12:2=6 см.

РК+МТ=6+6=12 см.

МК=12-8=4 см

Answer 2

Ответ:

Объяснение:

Отрезок средней линии трапеции между точками пересечения её с диагоналями равен полуразности оснований.

МК=(12-4)/2=8/2=4 см.