Question

Дан прямоугольный равнобедренный треугольник. Большая сторона равна 4. Найдите площадь треугольника

Answer 1

Ответ:

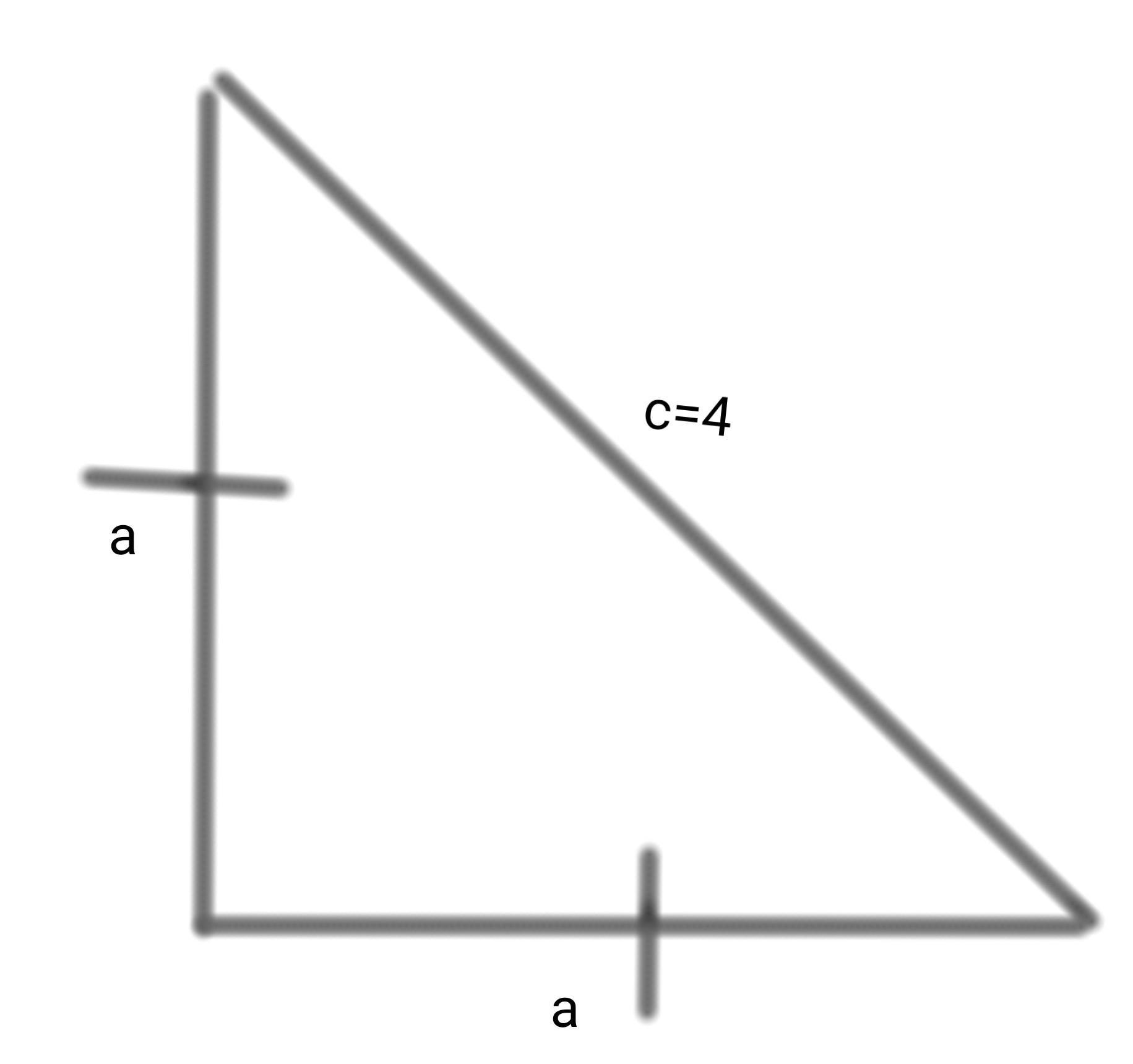
Гипотенуза c=4

Катеты a и a, потому что они равны.

По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов

${c}^{2} = {a}^{2} + {a}^{2} \\ {c}^{2} = 2 {a}^{2}$

${4}^{2} = 2 {a}^{2} \\ 16 = 2 {a}^{2} \\ {a}^{2} = 8 \\ a = 2 \sqrt{2}$

Площадь прямоугольного треугольника равен половине произведения катетов.

$S = \frac{1}{2} \times a \times a$

$S = \frac{1}{2} \times 2 \sqrt{2} \times 2 \sqrt{2} = 2 \times 2 = 4$

Площадь равен 4

Answer 2

Ответ:

Объяснение:

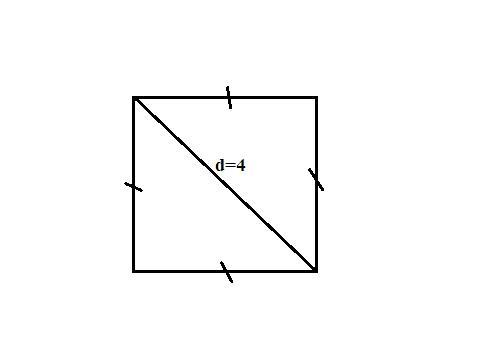
Площадь равнобедренного прямоугольного треугольника равна половине площади квадрата где диагональ - большая сторона. Площадь квадрата через диагонали:

S=d²/2 ⇒ Sтр.=d²/4=4²/4=4 ед².