Ответы
Ответ дал:
0
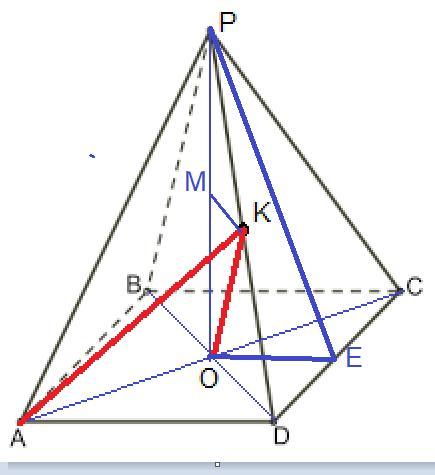
Сторона основания а = √64 = 8, половина диагонали основания АО = 4√2.
Так как отрезок КО лежит в плоскости DPO, перпендикулярной плоскости основания, в том числе и диагонали АС, то угол КОА равен 90 градусов.
Находим КО = АО*ctg(AKO) = 4√2*(√10/4) = √2*√10 = 2√5.
Так как КО - это медиана из прямого угла к гипотенузе, то гипотенуза (а это боковое ребро) равна двум медианам.
Значит, боковое ребро L равно 2*(2√5) = 4√5.
Высота пирамиды H = √(L² - (a/2)²) = √(16*5 - 16) = 8.
Апофема А = √(Н² + (а/2)²) = √(64 + 16) = √80 = 4√5.
Площадь боковой поверхности Sбок = (1/2)РА = (1/2)*(8*4)*4√5 = 64√5.
Площадь поверхности S = So + Sбок = 64 + 64√5 = 64(1 + √5).
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
