Question

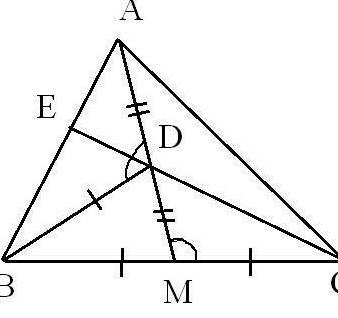
пусть АМ медиана трекгольника АВС, D середина отрезка АМ. Е точка пересечения прямой СD со стороной АВ. Оказалось что ВD равен ВМ. Докажите что угол ВАD равен углу MDC.


Очень прошу подробное решение с чертежом.​

Answer 1

Ответ:

D— середина отрезка AM⇒AD=DM

AM — медиана⇒BM=MC

BD = BM=MC⇒BD=MC

BD = BM⇒ΔBMD-равнобедренный⇒∠BMD=∠BDM

∠CMD=180°-∠BMD=180°-∠BDM=∠BDA⇒∠BDA=∠CMD

∠BDA=∠CMD; BD=MC; AD=DM⇒ΔBDA=ΔCMD⇒∠BAD = ∠MDC

ч.т.д

Объяснение:

г