Question

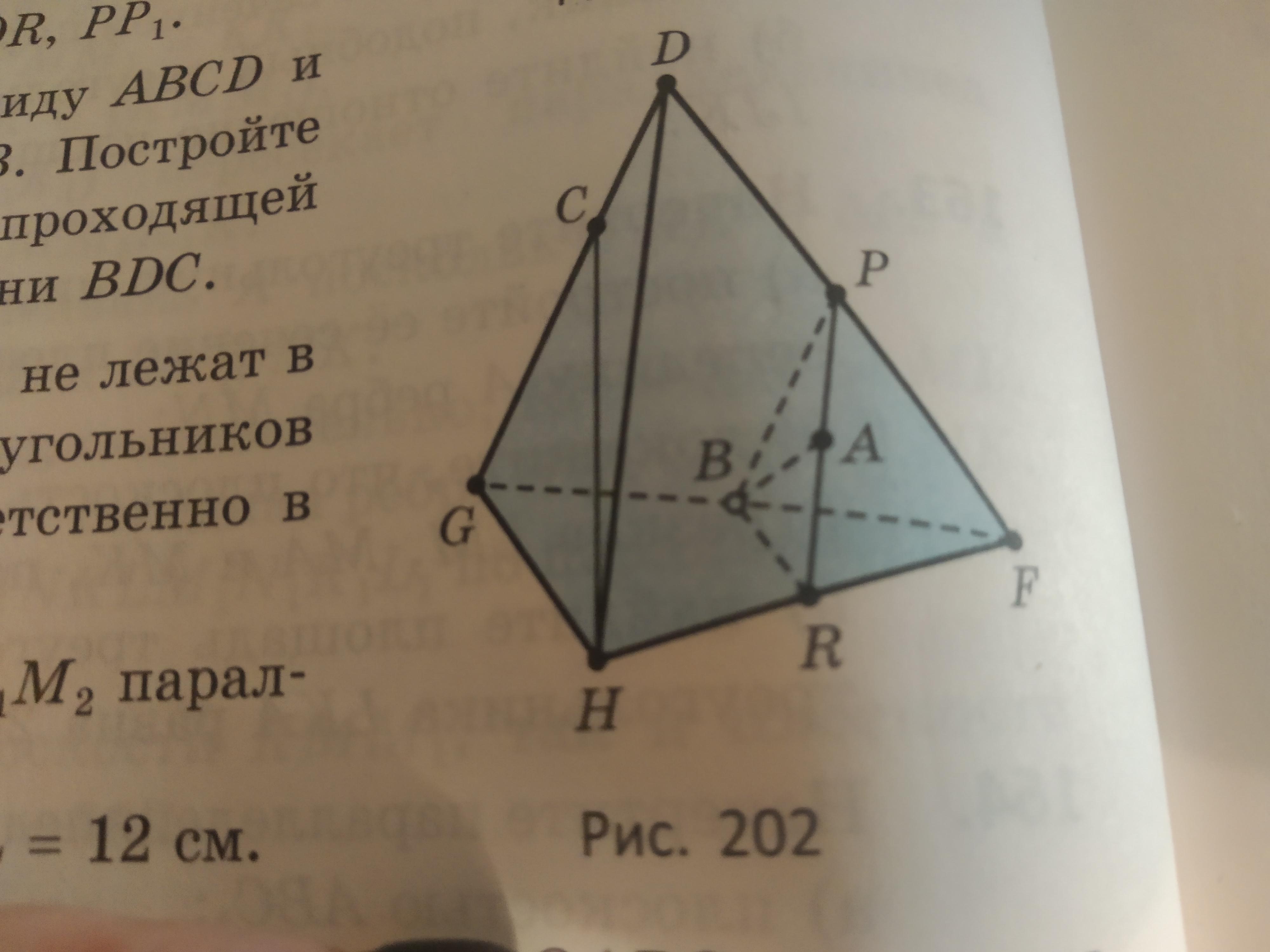
Учитывая,что точки B,P, R-середины ребер FG,FD,FH пирамиды DFGH,отрезок AB-медиана треугольника BPR,а точка C принадлежит ребру DG

a)докажите,что прямая AB параллельна плоскости DGH

б)установите, пересекаются ли прямая HC с плоскостью BPR

рисунок:

Answer 1

а) Тк точки B,P, R- середины ребер FG,FD,FH, то ВР и BR средние линии

∆GDF и ∆GHF. По свойству средних линий ВР||GC и BR||GH. Тогда (BPR) ||(GDН) по признаку параллельности двух плоскостей. Тогда любая прямая плоскости (BPR) , в частности ВА, будет параллельна плоскости (GDН).

б) Прямая HC с плоскостью (BPR) не пересекается, тк (BPR) ||(GDН) , а НС принадлежит (GDН).