Ответы
Ответ дал:
2
Ответ:
Объяснение:
Дано:
Найти:
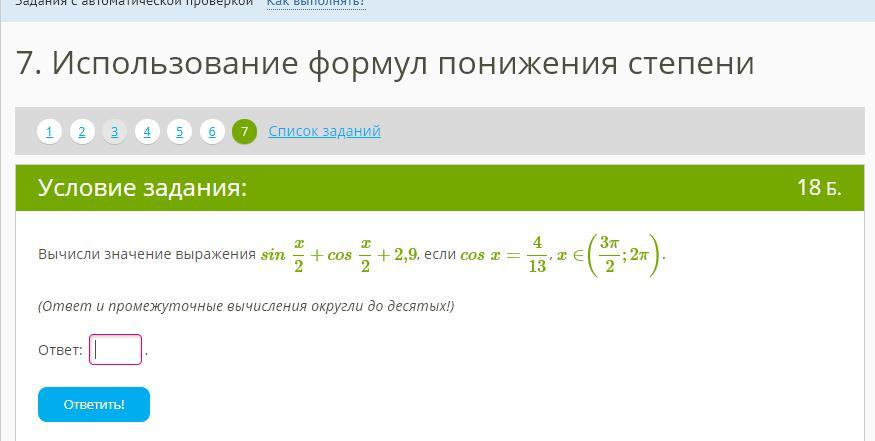
Решение:
Есть несколько ммм... стилей решения. Я пожалуй, предпочту наиболее наглядный, на мой взгляд.
Разделим решение на этапы.
a) Определим, в каких пределах лежит угол х/2 и какие у него значения синуса и косинуса:
b) Сделаем замену, с ней, на мой взгляд, проще:
c) Т.к. известен косинус 2a, а также знаки при синусе и косинусе угла a, вычисляем:
d) Решаем уравнение
e) Находим sin(a) cos(a), с учетом знаков + или -:
Округляем до десятых:
Вычисляем:
получили ответ: ≈ 2.7
ivankovryazhneckav:
Ответ неверный! Правильный ответ 2.6
не знаю, у меня 2,7 получается
Вообще-то, "правильный" ответ (с округлением до сотых) будет
0,588 - 0,809 + 2.9 = 2.9 - 0.221 = 2.679
А округляем 2.679 -> 2.68 -> 2.7
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад