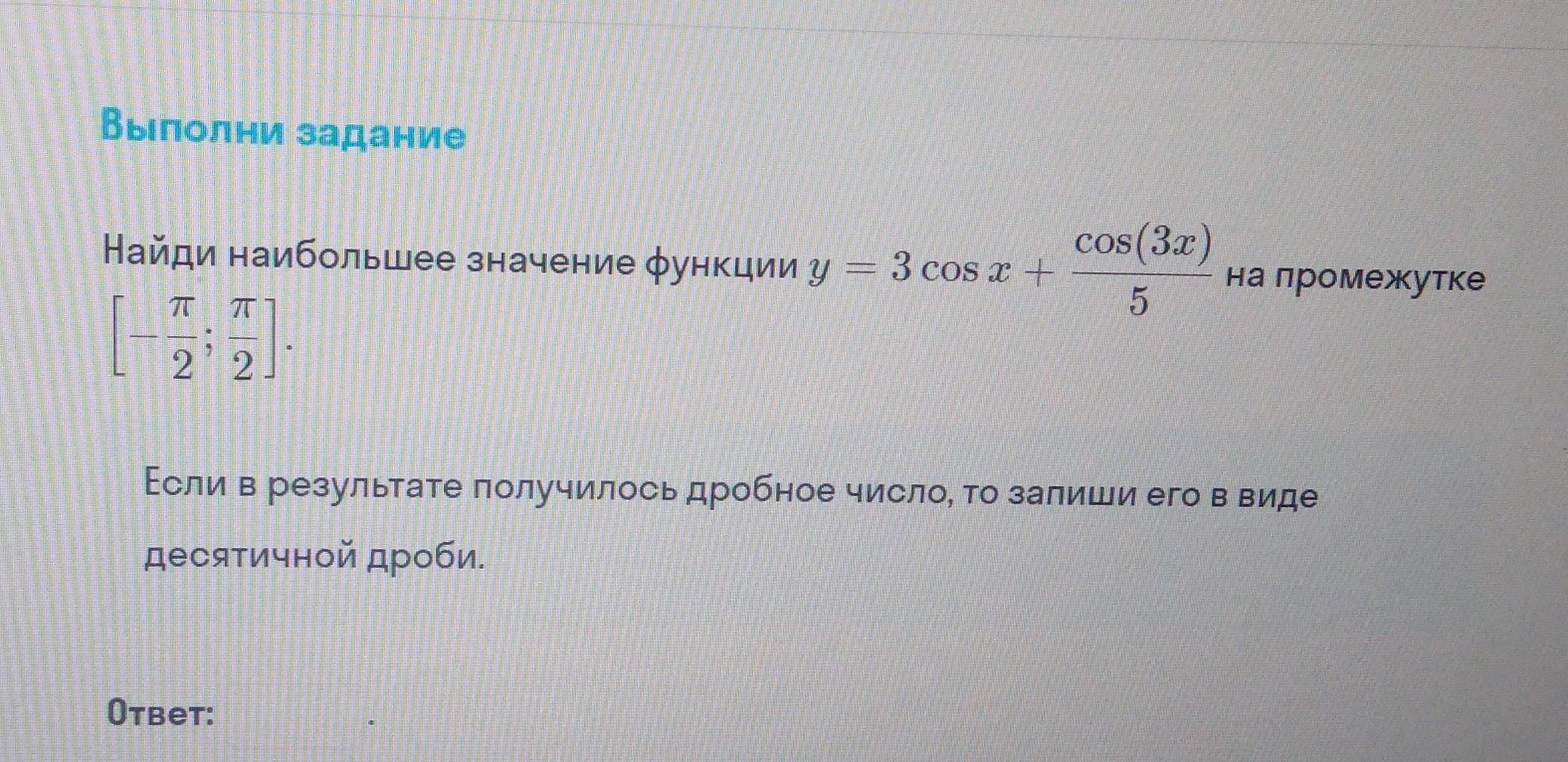
Ответы
Ответ дал:
1
Ответ:3.2
Объяснение:
При :
и
принимают свои наибольшие значения, а значит и функция принимает наибольшее значение равное 3.2
Ответ дал:
1
найдем производную функции. она равна -3sinx -3sin3x/5;
-3sinx -3sin3x/5=0; 5sinx +sin3x=0; 5sinx +3sinx-4sin³x=0;
8sinx -4sin³x=0;
4sinx* (2-sin²x)=0; если скобка равна нулю. то sinx=±√2. чего быть не может, поэтому sinx =0⇒х=πn; n∈Z
-π/2≤πn≤π/2; -1/2≤n≤1/2
n=0⇒ x=0 ∈[-π/2; π/2], найдем значение функции в точке х=0 и на концах указанного отрезка.
у(0)=3сos0+(cos(3*0))/5=3*1+1/5=3.2;
у(-π/2)=3*0+(cos(-3π/2))/5=0;
у(π/2)=3*0+(cos(3π/2))/5=0;
наименьшее значение в точках ±π/2, оно равно нулю.
наибольшее в точке х=0, оно равно 3.2
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
8 лет назад
10 лет назад