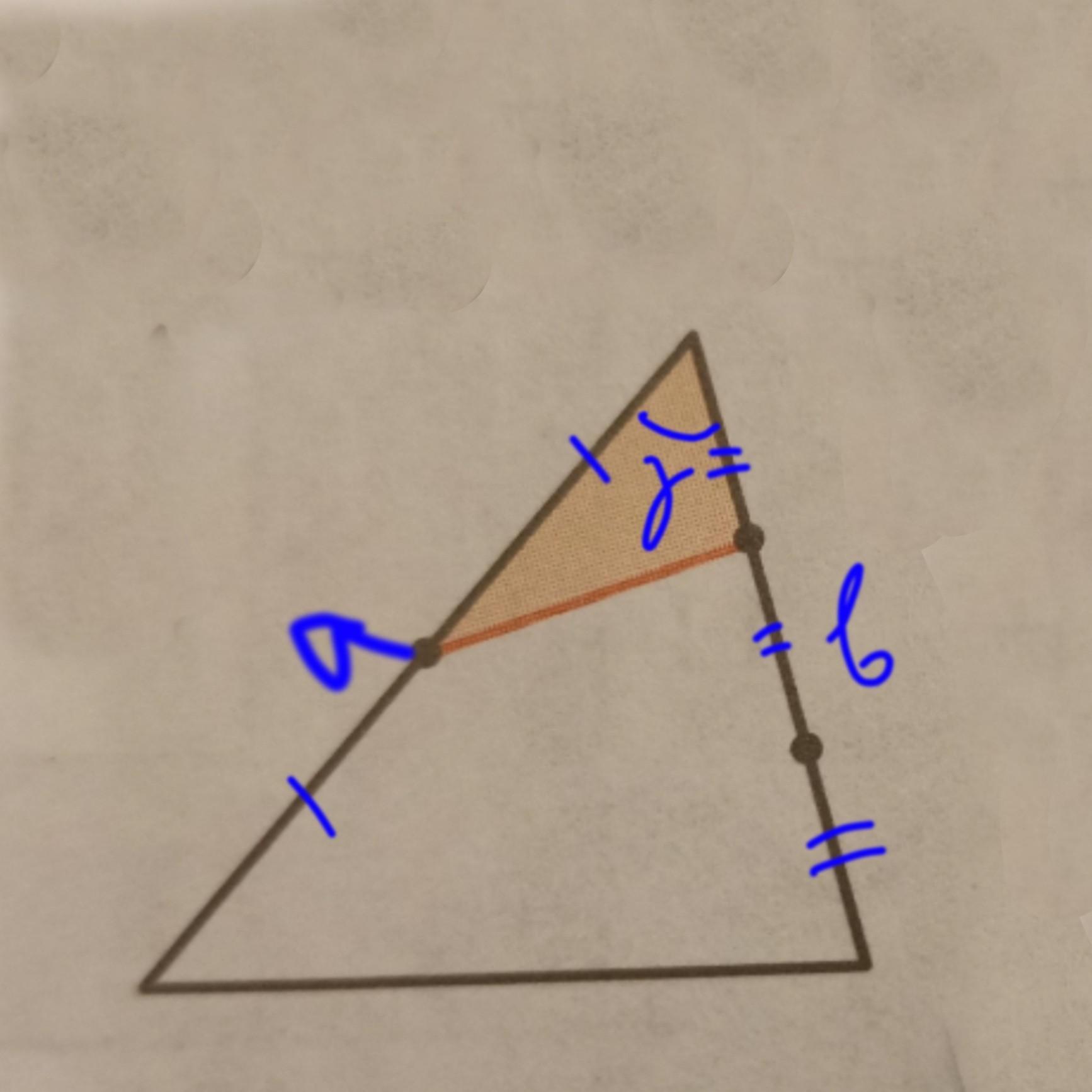
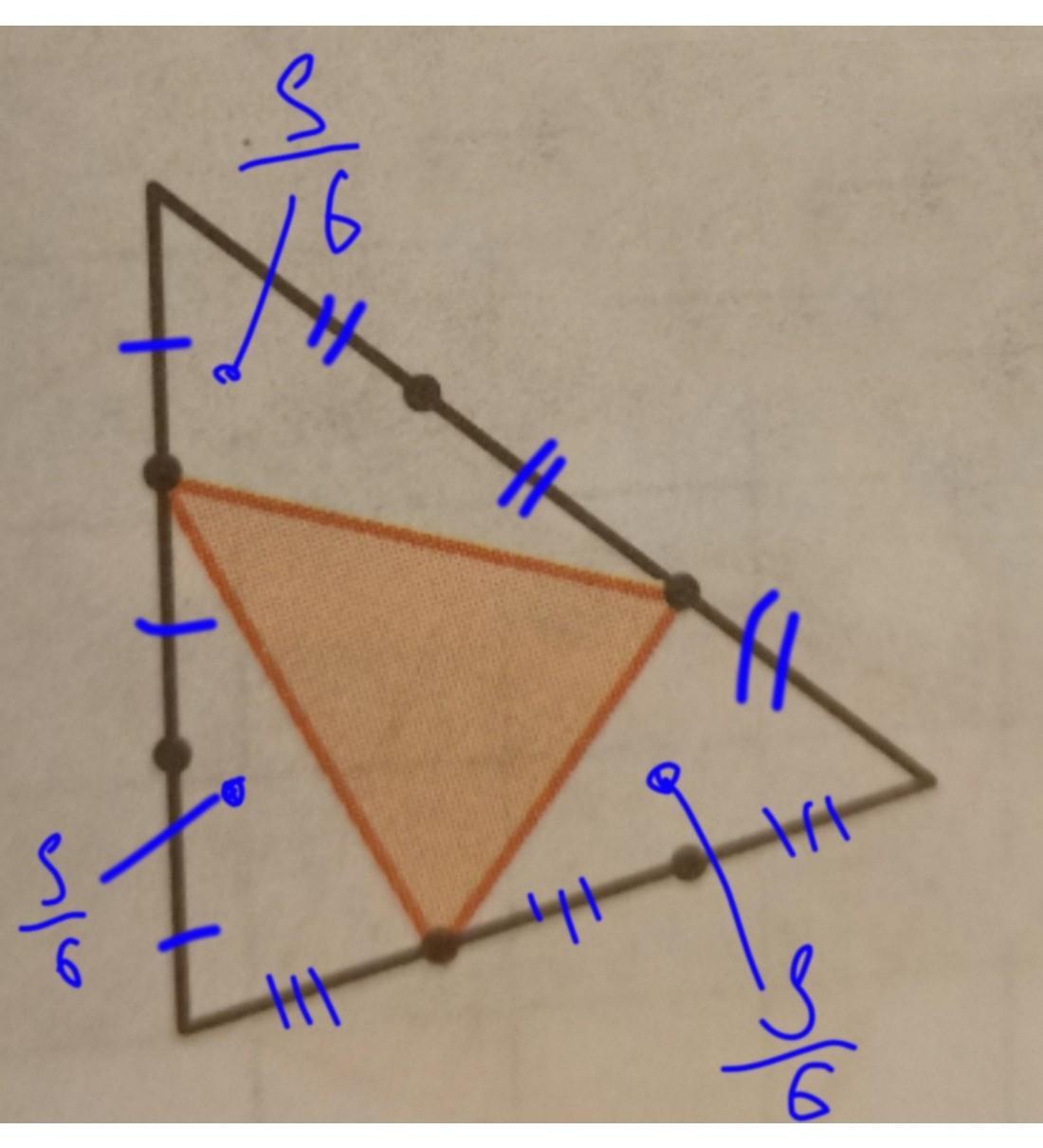
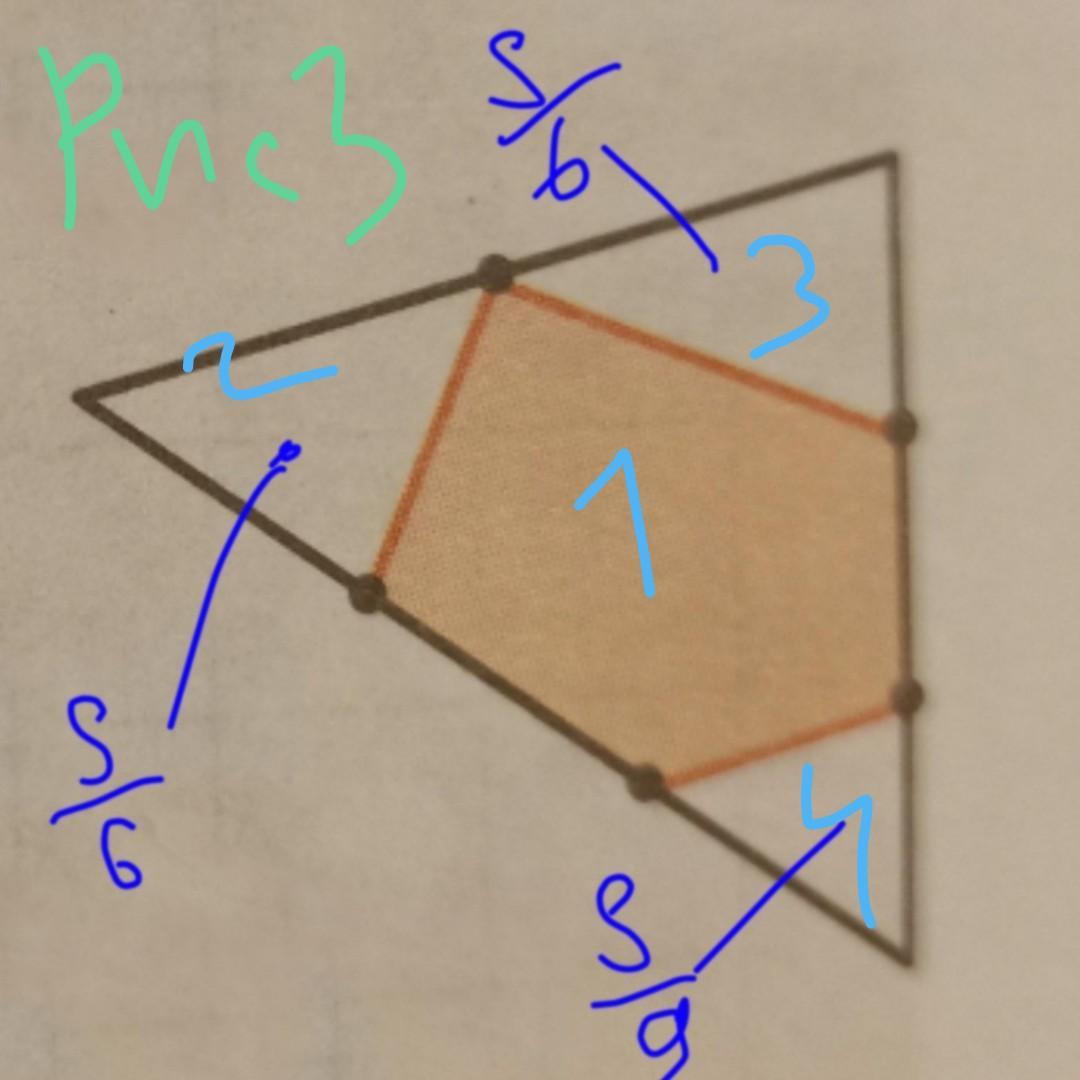
Площадь треугольника равна 1.Каждая его сторона отмеченными точками делится на равные части. Найдите площади закрашенных фигур на рисунке.
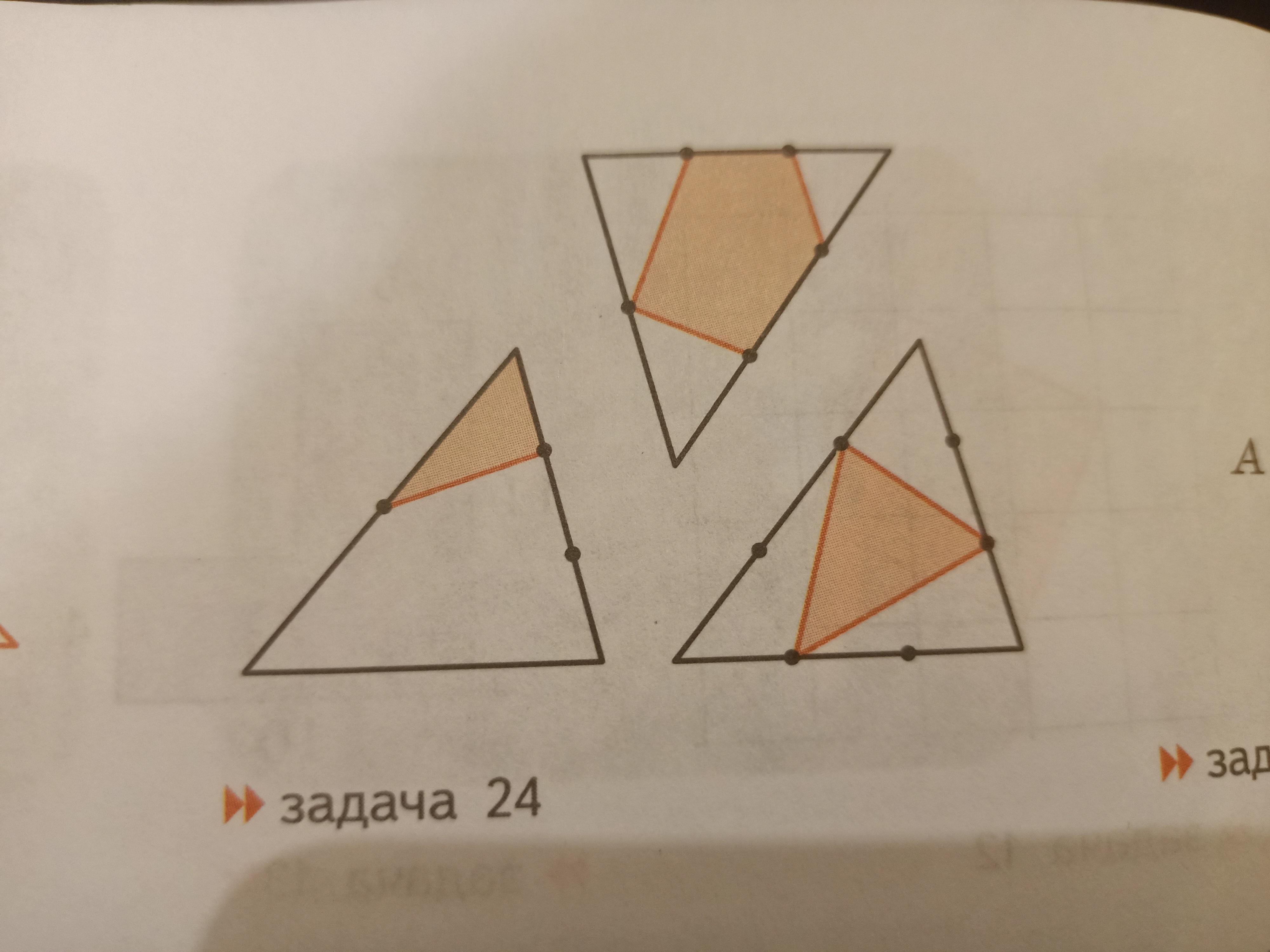
Ответы
Ответ:
1) S = 1/6
2) S = 1/2
3) S = 5/9
Объяснение:
Площадь треугольника можно вычислить по следующей формуле:
1) Обозначим площадь закрашенного ∆-ка S1 (см. рис.1)
Очевидно, т.к. точки делят стороны "единичного" ∆ка на равные отрезки, а угол у единичного и у малого треугольника общий, то
- общий
и площадь S1 равна
А т.к.
2) Пусть площадь закрашенной фигуры (а это - треугольник, см. рис.) равна S1.
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (обозначим их площади S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Треугольники 2, 3, 4 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Соответственно, искомая площадь составляет
3) Пусть площадь закрашенной фигуры (а это - шестиугольник, см. рис.) равна S1
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (пусть их площади будут S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Площади треугольников 2, 3 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Но площадь треугольника 4 меньше: у него две стороны втрое меньше чем у исходного единичного, потому его площадь равна:
Следовательно, общая площадь незакрашенных частей равна:
А искомая площадь закрашенной фигуры S1 составляет