Question

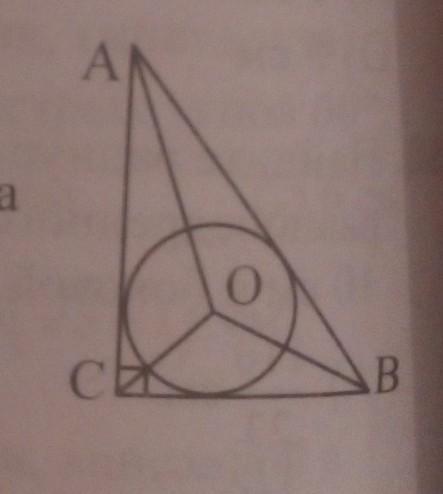
Найдите длину гипотенузы AB прямоугольного треугольника ABC, если точка 0-центр вписанной окружности, уголOBA=30° и BC+AB=12.
​

Answer 1

Ответ:

8

Пусть D-точка пересечения вписанной окружности и гипотенузы AB, E-точка пересечения вписанной окружности и катета BC.

В треугольнике ODB D=90°,OBD=30° =>OD=OB/2

OD=OE (оба диаметры окружности)=>OE=OB/2

В треугольнике OEC E=90°,OE=OB/2 => OBE=30°

CAB=90°-B=90°-(ABO+OBC)=90°-(30°+30°)=30°

В треугольнике ACB C=90°,CAB=30° => CB=AB/2

BC+AB=12

AB/2+AB=12

1,5AB=12

AB=12/1,5=8

Answer 2

Ответ:

Объяснение:

ΔАВС прямоугольный, ОВ - биссектриса (центр вписанной окружности лежит на пересечении биссектрис треугольника) ⇒ ∡В=30*2=60°, ∡А=90-60=30° ⇒ ВС=АВ/2 (катет прямоугольного треугольника против угла 30°);

АВ+ВС=12

АВ+АВ/2=12

3АВ=24

АВ=24/3=8 ед.