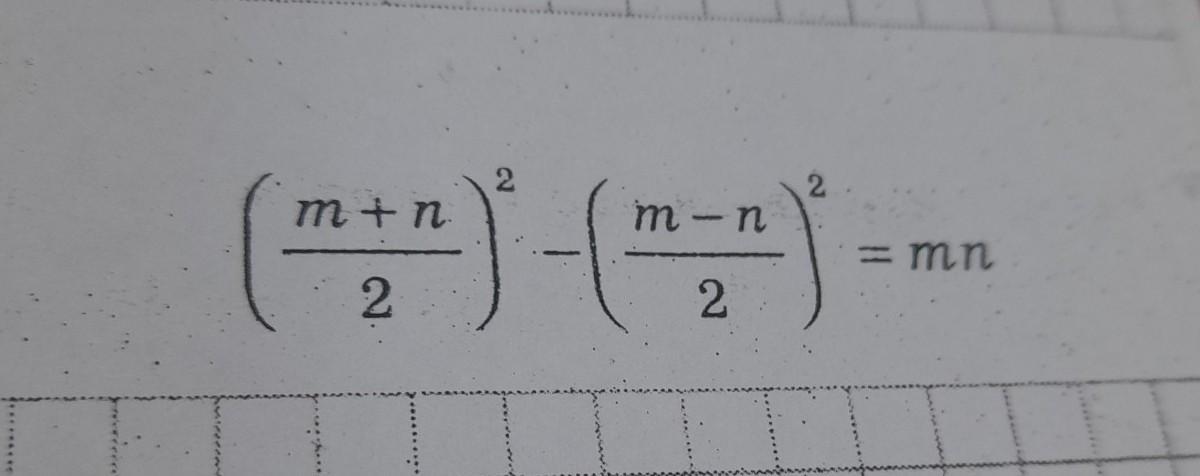Ответы
Ответ дал:
2
Пошаговое объяснение:
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
После преобразования левой части мы получили выражение, стоящее справа. Следовательно, они тождественны, и данное равенство - верно.
Ч. Т. Д.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад