Ответы
Ответ:
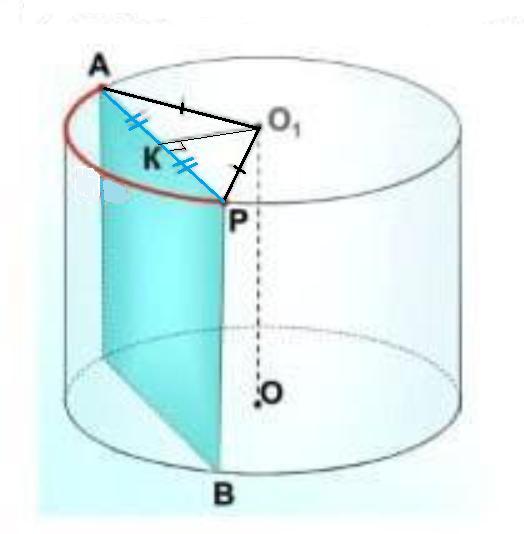
1) S (сечения)=240 дм² , H=OO₁=PB=10 дм , O₁K=9 дм .
Найти R .
Расстояние между прямой и параллельной ей плоскостью – это расстояние (длина перпендикуляра) от любой точки заданной прямой до заданной плоскости. По условию сечение параллельно оси цилиндра, поэтому расстоянием от оси до сечения будет отрезок O₁К , который перпендикулярен сечению, O₁К⊥АР .
Сечение - это прямоугольник, его площадь равна АР*РВ=АР*10=240 дм²,
АР=240:10=24 дм .
ΔАО1Р: АО₁=РО₁ как радиусы ⇒ ΔАО1Р - равнобедренный
По условию АК=КР ⇒ О₁К - высота ΔАО₁Р .
KP=AP:2=24:2=12 дм .
По теореме Пифагора: R²=PO₁²=KP²+KО₁²=12²+9²=225=15² ,
R=15 дм .
( Рисунок подходит тот же, что и для второй задачи. )
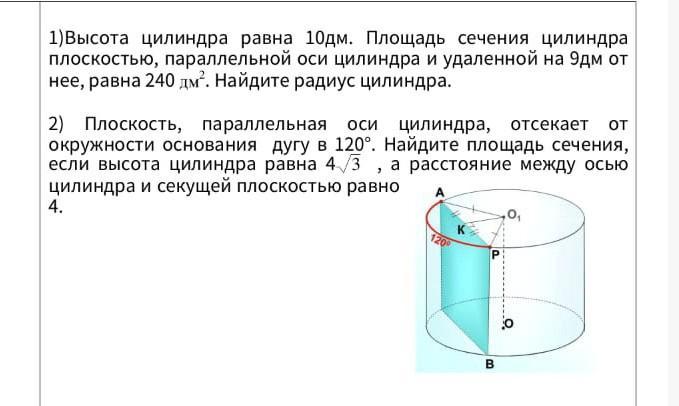
2) Дан цилиндр , H=OO₁=PB= , O₁K=4 (аналогично предыдущей задаче) , дуга АР=120° .
Найти S(сечения) .
Дуга в 120° соответствует центральному углу в 120° .
Значит ∠АО₁Р=120° .
ΔАО₁Р - равнобедренный, так как АО₁=РО₁=R .
АК=КР ⇒ КО₁ - медиана , высота и биссектриса ,
ΔКО₁Р - прямоугольный и ∠КО₁Р=60° ⇒ ∠КРО₁=30°
Против угла в 30° лежит катет, равный половине гипотенузы, значит гипотенуза РО₁ в 2 раза больше катета КО₁ , РО₁=4*2=8 ⇒ R=8 .
KP²=PО₁²-KО₁²=8²-4²=48 , KP=√48=4√3 .
AP=2*KP=8√3
S(сечения)=AP*PB=8√3*4√3=32*3=96 (ед²) .